Python数据结构与算法之链表,无序链表详解

目录

• 我们首先来构造节点。
• 节点（Node）的类构建完毕后，接下来我们开始构建整个链表（LinkList）的类。
• 那么我们还需要一个方法来判断链表头的指向。
• 接下来我们构建链表节点的添加方法。
• 实现length方法（计算链表中节点的个数/链表长度）
• 实现search方法（搜索链表中的某个节点）
• 实现remove方法（移除链表中的某个节点）
• 代码汇总
• 总结

链表是一系列元素的集合，这些元素的内存是散乱的。

无序链表则是一系列逻辑无序元素的集合，只是通过链表数据结构连接起来。虽然这些元素整体来看是散乱的，但其中每一个元素都有一个相对于其他元素的位置信息。所以链表需要维持元素之间的相对位置，但是也不需要特意在一段内存空间中存储这些位置信息。

以下图中的元素集合为例，这些元素的位置看上去都是随机的。如果可以为每一个元素附加一份信息，即下一个元素的位置，那么这些元素的相对位置就能通过自身指向下一个元素的链接来表示。

附加信息后则可表示为：

需要注意的是，使用链表时我们必须指明链表中第一个元素的位置。一旦知道第一个元素的位置，就能根据其中的链接信息访问第二个元素，接着访问第三个元素，依此类推。指向链表第一个元素的引用被称作头 。最后一个元素需要知道自己没有下一个元素。

认真观察链表，我们将每一个元素视为一个节点，链表则是通过他们之间的相对位置关系把这些节点串起来的。每一个节点至少包含了两个基本属性，首先就是节点的数据变量，其次就是节点对下一个节点位置的指向关系。

我们首先来构造节点。

节点（Node）是构建链表的基本数据结构。每一个节点对象都必须持有至少两份信息。首先，节点必须包含一个数据元素，我们称之为节点的数据变量 。其次，节点必须保存指向下一个节点的引用。下面的代码展示了 Node 类的Python实现。在构建节点时，需要为其提供初始值。Node 类也需要包含访问和修改数据的方法，以及指向下一 个元素的引用。

class Node:
    def __init__(self, initdata):
        self.data = initdata  # 数据元素
        self.next = None      # 指向下一节点的引用
    def getData(self):
        return self.data
    def getNext(self):
        return self.next
    def setData(self, newdata):
        self.data = newdata
    def setNext(self, newnext):
        self.next = newnext

需要注意的是，None 在 Node 类以及之后的链表中起到了重要的作用。节点指向 None 的引用代表着后面没有新节点。所以，在 Node 的构造方法中我们将 next 的初始值设为 None 。

节点（Node）的类构建完毕后，接下来我们开始构建整个链表（LinkList）的类。

如前所述，链表是基于节点集合来构建的，每一个节点都通过显式的引用指向下一个节点。只要知道第一个节点的位置（第一个节点包含第一个元素），其后的每一个元素都能通过对下一个节点的引用找到。因此，LinkList 类必须包含指向第一个节点的引用。下列代码展示了 LinkList 类的构造方法。

class LinkList:
    def __init__(self):
        self.head = None

下图展示了链表无节点和有节点的两种情况：

我们已经有了链表头的创建方法，我们规定链表头的初始指向为None，当链表中有内容（节点）时，链表头则指向节点。

那么我们还需要一个方法来判断链表头的指向。

我们使用 isEmpty 方法检查链表的头部是否为指向None的引用。布尔表达式 self.head == None 当且仅当链表中没有节点时才为真。由于新的链表是空的，因此构造方法必须和检查是否为空的方法保持一致。这体现了使用 None 表示链表末尾的好处。

class LinkList:
    def isEmpty(self):
        return self.head == None

接下来我们构建链表节点的添加方法。

为了将节点添加到链表中，我们需要实现 add 方法。但在实现之前，需要解决一个重要问题：新节点要被放在链表的哪个位置？由于链表是无序元素的集合，因此新元素相对于已有元素的位置并不重要。新的元素可以在任意位置。因此，将新元素放在最简便的位置是最合理的选择。 由于链表只提供一个入口（头部），因此其他所有节点都只能通过第一个节点以及 next 链接来访问。这意味着添加新节点最简便的位置就是头部，或者说是链表的起点位置。我们把新节点作为链表的第一个节点，并且把已有的节点链接到该元素的后面。

下列代码展示了 add 方法的实现：

class LinkList:
    def add(self, item):
        temp = Node(item)
        temp.setNext(self.head)
        self.head = temp

代码第 3 行创建一个新节点，并且将 item 作为其数据。现在需要将新节点与已有的链表结构链接起来。这一过程需要两步，如下图所示。图中第 1 步（代码第 4 行），将新节点的 next 引用指向当前链表中的第一个节点。 这样一来，原来的链表就和新节点正确地链接在了一起。图中第 2 步，修改链表头的指向， 使其指向新创建的节点。代码第 5 行的赋值语句，完成了这一操作。

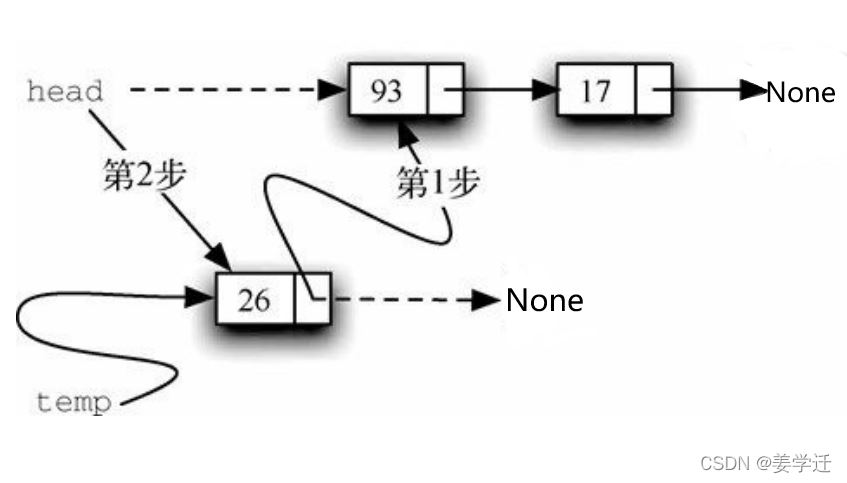
上述两步的顺序非常重要。如果颠倒代码第 4 行和第 5 行的顺序，会发生什么呢？如果先修改链表头的指向，由于头节点是唯一指向链表节点的外部引用，因此所有的已有节点都将丢失并且无法访问。

接下来我们要实现的方法还有 length 、search 以及 remove ，这些方法都基于遍历链表。遍历是指系统地访问每一个节点，具体做法是额外用一个外部引用从链表的头节点开始访问。随着访问每一个节点，我们将这个外部引用通过“遍历”下一个引用来指向下一个节点。

实现length方法（计算链表中节点的个数/链表长度）

class LinkList:
    def length(self):
        current = self.head
        count = 0
        while current != None:
            count = count + 1
            current = current.getNext()
        return count

为了实现 length 方法，需要遍历链表并且记录访问过多少个节点。上述代码展示了计算链表中节点个数的Python代码。current 就是外部引用，它在第 3 行中被初始化为链表头的引用。此时如果链表中没有节点，current 将指向 None，如果链表中有节点，current 此时就是指向链表中的第一个结点。

在计算开始时，由于没有访问到任何节点，因此 count 被初始化为 0 。第 5~7 行实现遍历过程。只要 current 指向的不是链表的结尾（None），就将它指向下一个节点（第 7 行）。每当current 指向一个新节点时，将count加 1。最终，循环完成后返回 count 。

实现search方法（搜索链表中的某个节点）

在链表中搜索一个值同样也会用到遍历。每当访问一个节点时，检查该节点中的元素是否与要搜索的元素相同。在搜索时，可能并不需要完整遍历链表就能找到该元素。事实上，如果遍历到链表的末尾，就意味着要找的元素不在链表中。如果在遍历过程中找到所需的元素，就没有必要继续遍历了。

class LinkList:
    def search(self, item):
        current = self.head
        found = False
        while current != None and not found:
            if current.getData() == item:
                found = True
            else:
                current = current.getNext()
        return found

上述代码展示了 search 方法的实现。与在 length 方法中相似，遍历从列表的头部开始（第3行）。我们使用布尔型变量 found 来标记是否找到所需的元素。由于一开始时并未找到该元素，因此第 4 行将 found 初始化为False 。

第 5 行的循环既考虑了是否到达链表末尾，也考虑了是否已经找到目标元素。只要还有未访问的节点并且还没有找到目标元素，就继续检查下一个节点。第 6 行检查当前节点中的元素是否为目标元素。如果是，就将 found 设为True。

实现remove方法（移除链表中的某个节点）

remove 方法在逻辑上需要分两步。

第 1 步，遍历列表并查找要移除的元素(节点)。一旦找到该元素（假设元素在链表中），就必须将其移除。第 1 步与 search 非常相似。从一个指向链表头节点的外部引用开始，遍历整个链表，直到遇到需要移除的元素。假设目标元素已经在链表中，因此我们预测循环会在 current 抵达 None 之前结束。这意味着可以在判断条件中使用布尔型变量 found 。

第 2 步，移除元素(节点)。当 found 被设为 True 时，current 将指向需要移除的节点。该如何移除它呢？一种做法是将节点包含的值替换成表示其已被移除的标识值（比如 None 或者 Null，完全可以自定义）。这种做法的问题是，节点的数量和元素的数量不再匹配。更好的做法是移除整个节点。

为了将包含元素的整个节点移除，需要将其前面的节点中的 next 引用指向 current 之后的节点。然而，并没有反向遍历链表的方法。由于current 已经指向了需要修改的节点之后的节点，此时做修改为时已晚。

这一困境的解决方法就是在遍历链表时使用两个外部引用。current 与之前一样，标记在链表中的当前位置。新的引用 previous 总是指向 current 上一次访问的节点。这样一来，当current 指向需要被移除的节点时，previous 就刚好指向真正需要修改的节点。

class LinkList:
    def remove(self, item):
        current = self.head
        previous = None
        found = False
        while not found:
            if current.getData() == item:
                found = True
            else:
                previous = current
                current = current.getNext()
                if current == None:
                	return found
        if previous == None:
            self.head = current.getnext()
        else:
            previous.setNext(current.getNext())

上面的代码展示了完整的 remove 方法。第 3~4 行对两个引用进行初始赋值。注意，current 与其他遍历例子一样，从链表的头节点开始。由于头节点之前没有别的节点，因此 previous 的初始值是None。

第 7~8 行检查当前节点中的元素是否为要移除的元素。如果是，就设 found 为 True 。 如果不是，则将 previous 和 current 往下一个节点的方向各移动一次。这两条语句的顺序十分重要。必须先将 previous 移动到current 的位置，然后再移动 current。这一过程经常被称 为“蠕动”，因为 previous 必须在 current 移动之前指向其当前位置。

下图展示了这一过程：

一旦搜索过程结束，就需要执行移除操作。如移除图中数据值为 17 的节点，修改过程如下：

有一种特殊情况需要注意，如果被移除的节点正好是链表的第一个节点，那么 current 会指向链表中的第一个节点，previous 的值则是None 。在这种情况下，需要修改链表的头节点，而不是 previous 指向的节点，如图所示：

代码第 13 行检查是否遇到上述特殊情况。如果 previous 没有移动，当 found 被设为True 时，它的值仍然是None 。在这种情况下 （第13行），链表的头节点指向被修改成指向当前头节点的下一个节点，从而达到移除头节点的效果。但是，如果 previous 的值不是None ，则说明需要移除的节点在链表结构中的某个位置。在这种情况下，previous 指向了 next 引用需要被修改的节点。第 16 行使用 previous 的 setNext 方法来完成移除操作。注意，在两种情况中，修改后的引用都指向current.getNext() 。

代码汇总

# 构造节点
class Node:
    def __init__(self, initdata):
        self.data = initdata      # 数据元素
        self.next = None          # 指向下一节点的引用（python变量赋值的本质是引用）
    def getData(self):            # 获取节点的数据元素值
        return self.data
    def getNext(self):            # 获取下一节点的引用 若有节点则直接视作为下一节点
        return self.next
    def setData(self, newdata):   # 给节点的数据元素设置值
        self.data = newdata
    def setNext(self, newnext):   # 给节点设置对下一节点的引用
        self.next = newnext

# 构造链表
class LinkList:
    def __init__(self):            # 设置链表的头部指向 无节点时为None
        self.head = None
    def isEmpty(self):             # 判断链表是否为空（是否有节点）
        return self.head == None
    def add(self, item):           # 给链表增加新节点（从链表头位置增加）
        temp = Node(item)            # 创建节点并对新节点数据元素赋值
        temp.setNext(self.head)      # 新节点指向当前链表中的第一个节点
        self.head = temp             # 链表头指向新节点
    def length(self):               # 计算链表长度（节点个数）
        current = self.head           # 引入current作为指向标识 指向第一个节点 或者None
        count = 0                     # 引入count作为计数变量
        while current != None:        # 当指向标识指向的不是链表末尾的None时
            count = count + 1           # 节点计数加一
            current = current.getNext() # 指向标识向后移动
        return count
    def search(self, item):                   # 搜索链表中节点
        current = self.head                     # 引入current作为指向标识 指向第一个节点
        found = False                           # 引入found作为寻找状态标识
        while current != None and not found:    # 当current没有指向None 并且 未找到节点
            if current.getData() == item:         # 如果current当前指向的节点是寻找的节点
                found = True                        # 找到
            else:                                 # 否则
                current = current.getNext()         # 指向标识向后移动
        return found
    def remove(self, item):                 # 从链表中移除节点
        current = self.head                   # 引入current指向标识指向第一个节点
        previous = None                       # 引入previous指向标识指向current的上一个节点 所以当current指向第一个节点时 previous初始化指向的是None
        found = False                         # 引入寻找状态标识 寻找需要移除的节点
        while not found:                      # 遍历节点 以找到为循环结束条件
            if current.getData() == item:       # 如果当前节点是目标节点
                found = True                      # 找到
            else:                               # 当前节点不是目标节点
                previous = current                # previous指向当前节点
                current = current.getNext()       # current指向移动到下一个节点
                if current == None:               # 如果到最后都没找到目标节点
                    return found
                                              # 搜索过程结束
        if previous == None:                  # 如果previous目前指向的是None 代表current指向的是链表的第一个节点 也就是说删除的目标节点就是第一个节点
            self.head = current.getnext()        # 链表头直接指向None表示删除第一个节点
        else:                                 # 其他情况下
            previous.setNext(current.getNext())  #  当前节点的上一个节点指向当前节点的下一个节点

无注释版：

class Node:
    def __init__(self, initdata):
        self.data = initdata
        self.next = None
    def getData(self):
        return self.data
    def getNext(self):
        return self.next
    def setData(self, newdata):
        self.data = newdata
    def setNext(self, newnext):
        self.next = newnext

class LinkList:
    def __init__(self):
        self.head = None
    def isEmpty(self):
        return self.head == None
    def add(self, item):
        temp = Node(item)
        temp.setNext(self.head)
        self.head = temp
    def length(self):
        current = self.head
        count = 0
        while current != None:
            count = count + 1
            current = current.getNext()
        return count
    def search(self, item):
        current = self.head
        found = False
        while current != None and not found:
            if current.getData() == item:
                found = True
            else:
                current = current.getNext()
        return found
    def remove(self, item):
        current = self.head
        previous = None
        found = False
        while not found:
            if current.getData() == item:
                found = True
            else:
                previous = current
                current = current.getNext()
				if current == None:
					return found
        if previous == None:
            self.head = current.getnext()
        else:
            previous.setNext(current.getNext())

代码运行结果如下图：

总结

本篇文章就到这里了，希望能够给你带来帮助，也希望您能够多多关注我们的更多内容!