Python PCA降维的两种实现方法

目录

• 前言
• PCA降维的一般步骤为：
• 实现PCA降维，一般有两种方法：
• 总结

前言

PCA降维，一般是用于数据分析和机器学习。它的作用是把一个高维的数据在保留最大信息量的前提下降低到一个低维的空间，从而使我们能够提取数据的主要特征分量，从而得到对数据影响最大的主成分，便于我们对数据进行分析等后续操作。

例如，在机器学习中，当你想跟据一个数据集来进行预测工作时，往往要采用特征构建、不同特征相乘、相加等操作，来扩建特征，所以，当数据处理完毕后，每个样本往往会有很多个特征，但是，如果把所有数据全部喂入模型，可能会导致糟糕的结果。在高维数据集中，往往只有部分特征有良好的预测能力，很多特征纯粹是噪音(没有预测能力)，很多特征彼此之间也可能高度相关，这些因素会降低模型的预测精度，训练模型的时间也更长。降低数据集的维度在某种程度上能解决这些问题，这时候就用到了PCA降维。

假设原始数据集的特征有500个，通过PCA降维，降到了400，那么我们就可以用降维后得到的这400个特征代替原始数据集的那500个，此时再喂给模型，那么模型的预测能力相比之前会有所提升。但要明白一点的是，降维后得到的这400个特征是新的特征，是原始数据集在高维空间某一平面上的投影，能够反映原特征提供的大部分信息，并不是指在原来的500个中筛选400个特征。

PCA降维的一般步骤为：

1.将原始数据进行标准化（一般是去均值，如果特征在不同的数量级上，则还要将其除以标准差）

2.计算标准化数据集的协方差矩阵

3.计算协方差矩阵的特征值和特征向量

4.保留最重要（特征值最大）的前k个特征（k就表示降维后的维度）

5.找到这k个特征值对应的特征向量

6.将标准化数据集乘以该k个特征向量，得到降维后的结果

实现PCA降维，一般有两种方法：

首先先来解释一下代码中用到的数据集：

在这两个代码中，用的是sklean库中自带的iris（鸢尾花）数据集。iris数据集包含150个样本，每个样本包含四个属性特征（花萼长度、花萼宽度、花瓣长度、花瓣宽度）和一个类别标签（分别用0、1、2表示山鸢尾、变色鸢尾和维吉尼亚鸢尾）。

data = load_iris()
y = data.target
x = data.data

y就表示数据集中的类别标签，x表示数据集中的属性数据。因为鸢尾花类别分为三类，所以我们降维后，要跟据y的值，分别对这三类数据点进行绘图。

第一种，就是依照上面PCA的步骤，通过矩阵运算，最终得到降维后的结果：

import numpy as np
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt

def pca(dataMat, topNfeat):
    meanVals = np.mean(dataMat, axis=0)
    meanRemoved = dataMat - meanVals  # 标准化（去均值）
    covMat = np.cov(meanRemoved, rowvar=False)
    eigVals, eigVets = np.linalg.eig(np.mat(covMat))  # 计算矩阵的特征值和特征向量
    eigValInd = np.argsort(eigVals)  # 将特征值从小到大排序，返回的是特征值对应的数组里的下标
    eigValInd = eigValInd[:-(topNfeat + 1):-1]  # 保留最大的前K个特征值
    redEigVects = eigVets[:, eigValInd]  # 对应的特征向量
    lowDDatMat = meanRemoved * redEigVects  # 将数据转换到低维新空间
    # reconMat = (lowDDatMat * redEigVects.T) + meanVals  # 还原原始数据
    return lowDDatMat

def plotPCA(lowMat):
    reconArr = np.array(lowMat)
    red_x, red_y = [], []
    blue_x, blue_y = [], []
    green_x, green_y = [], []
    for i in range(len(reconArr)):
        if y[i] == 0:
            red_x.append(reconArr[i][0])
            red_y.append(reconArr[i][1])
        elif y[i] == 1:
            blue_x.append(reconArr[i][0])
            blue_y.append(reconArr[i][1])
        else:
            green_x.append(reconArr[i][0])
            green_y.append(reconArr[i][1])
    plt.scatter(red_x, red_y, c='r', marker='x')
    plt.scatter(blue_x, blue_y, c='b', marker='D')
    plt.scatter(green_x, green_y, c='g', marker='.')
    plt.show()

if __name__ == '__main__':
    data = load_iris()
    y = data.target
    x = data.data
    matx = np.mat(x)
    lowDMat = pca(matx, 2)
    plotPCA(lowDMat)

第二种，是在sklearn库中调用PCA算法来实现：

import matplotlib.pyplot as plt
from sklearn.decomposition import PCA  # 加载PCA算法包
from sklearn.datasets import load_iris
import numpy as np

data = load_iris()
y = data.target
x = data.data
pca = PCA(n_components=2)  # 加载PCA算法，设置降维后主成分数目为2
reduced_x = pca.fit_transform(x)  # 对样本进行降维
# reduced_x = np.dot(reduced_x, pca.components_) + pca.mean_  # 还原数据

red_x, red_y = [], []
blue_x, blue_y = [], []
green_x, green_y = [], []
# print(reduced_x)
for i in range(len(reduced_x)):
    if y[i] == 0:
        red_x.append(reduced_x[i][0])
        red_y.append(reduced_x[i][1])
    elif y[i] == 1:
        blue_x.append(reduced_x[i][0])
        blue_y.append(reduced_x[i][1])
    else:
        green_x.append(reduced_x[i][0])
        green_y.append(reduced_x[i][1])
plt.scatter(red_x, red_y, c='r', marker='x')
plt.scatter(blue_x, blue_y, c='b', marker='D')
plt.scatter(green_x, green_y, c='g', marker='.')
plt.show()

在第二个代码中，值得一说的是fit_transform()这个函数，它其实就是fit()和transform()这两个函数的结合，相当于先调用fit()再调用transform()。fit()和transform()这两个函数在sklearn库中经常出现，fit()函数可以理解为求传入的数据集的一些固有的属性（如方差、均值等等），相当于一个训练过程，而transform()函数，可以理解为对训练后的数据集进行相应的操作（如归一化、降维等等）。在不同的模块中，这两个函数的具体实现也不一样，比如在PCA模块里，fit()相当于去均值，transform()则相当于降维。

这两种代码运行后，生成的图像如下（图一为第一种代码，图二为第二种代码）：

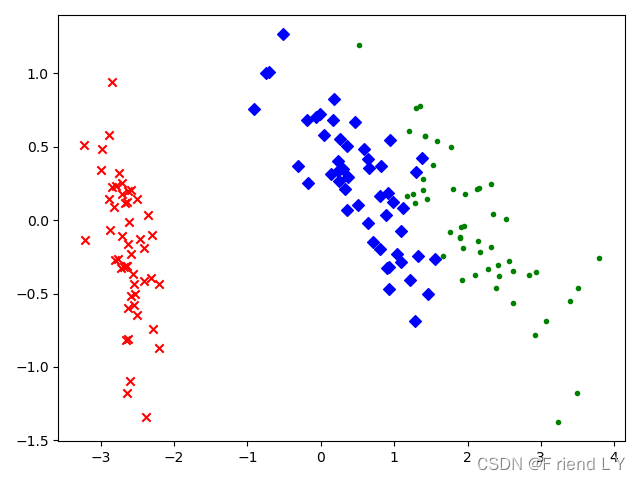
图一

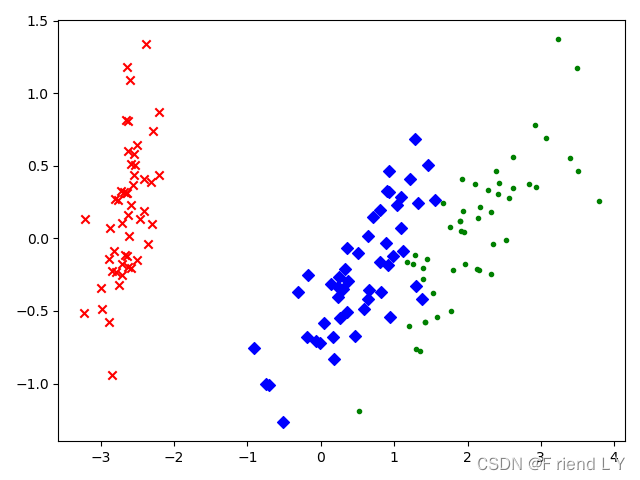
图二

可以看到，第一种代码画出的图像与第二种代码画出的图像关于y=0这条直线对称，虽然不清楚这是什么原因（后续有空的话我会去找找原因），但是这并不影响降维的结果。

降维前的数据（部分）：

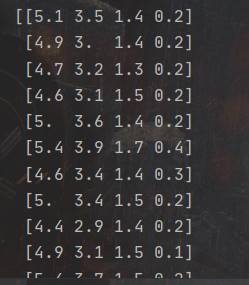
降维后的数据（部分）：

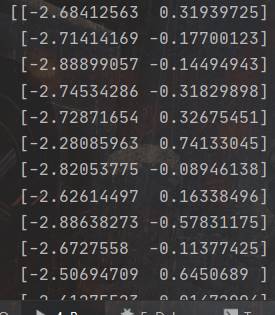
所以，此时我们使用降维后的二维数据集就可以用来表示降维前四维数据集的大部分信息。

降维后得到的数据可以通过逆操作来进行数据集的还原，具体原理就不过多解释，具体操作代码的话我已在代码的注释里面写出，但是重建出来的数据会和原始数据有一定的误差（如下图）

原因的话你可以这样理解：我们的原始数据为四维空间，现在用PCA降维到二维空间，则保留数据投影方差最大的两个轴向，因此舍弃掉了另外两个相对不重要的特征轴，从而造成了一定的信息丢失，所以会产生重构误差。

总结

到此这篇关于Python PCA降维的两种实现方法的文章就介绍到这了,更多相关Python PCA降维内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！