python实现高斯模糊及原理详解

高斯模糊是一种常见的模糊技术，相关知识点有：高斯函数、二维卷积。

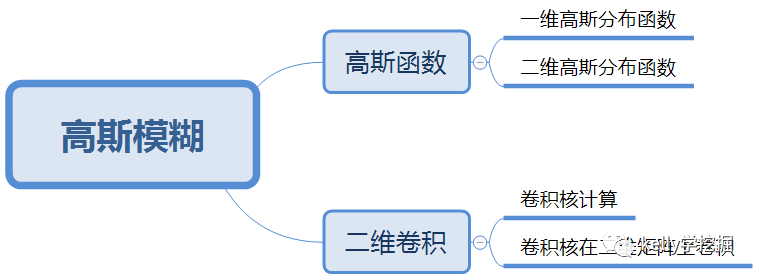
（一）一维高斯分布函数

一维（连续变量）高斯函数形式如下，高斯函数又称“正态分布函数”：

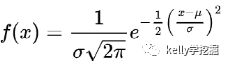
μ是分布函数的均值（或者期望），sigma是标准差。

一维高斯分布函数的图形：

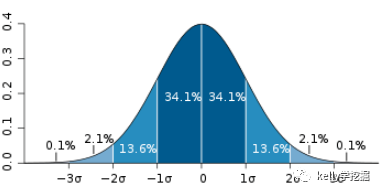
从图可知，以x=0为中心，x取值距离中心越近，概率密度函数值越大，距离中心越远，密度函数值越小。

（二）二维高斯分布函数

二维高斯分布函数的形式：

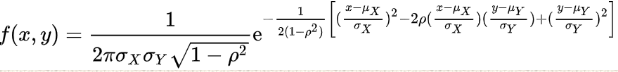
特别说明，当变量x和y相互独立时，则相关系数ρ=0，二维高斯分布函数可以简化为：

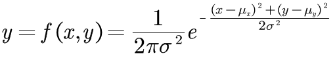
二维高斯分布函数的图形：

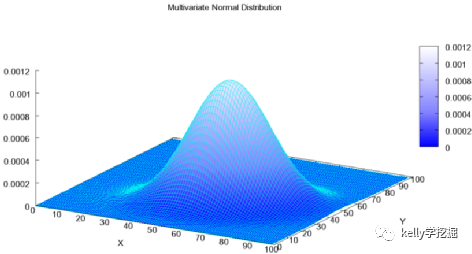
对于一维高斯分布，函数中心是平面上的一个点；而对于二维高斯分布，函数中心是一个三维立体空间上的一个点，即上图中山峰的最顶端处的点。

（三）高斯模糊

高斯模糊本质上一种数据平滑技术，可以用于一维、二维甚至多维空间。数据经高斯模糊处理之后，数据会趋向于周边邻近的其他数据，导致各个数据“趋同”。

在图像领域，各个位置的像素值使用“周边邻居像素点加权平均”重新赋值。对于每个像素点，由于计算时均以当前像素点为中心，所以均值μ=0。使用时有2个超参数需要设置：高斯核大小和高斯函数标准差σ。高斯核大小表示“影响当前点的最大邻域范围”，而标准差表示“邻域中的其他像素点对当前点的影响力”。

从下而上观察下图各个函数图像，各个函数的均值相同，而方差逐步减小。

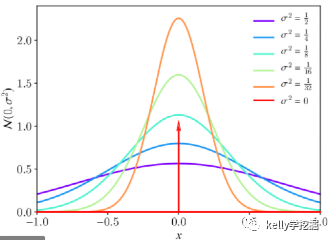
方差衡量数据的分散程度，方差越大，数据越分散，图形就越扁平，数据的集中趋势越弱，应用到高斯模糊中方差越大图形越模糊。

高斯模糊涉及到2个关键技术点：

（1）如何计算高斯卷积核

3×3大小的高斯卷积核的计算示意图

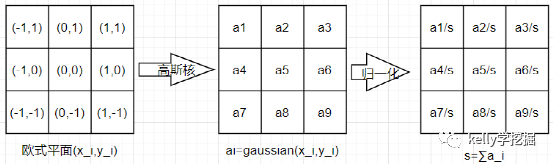
直接计算二维高斯函数值后，卷积核的各个位置取值（截图自pycharm的debug）：

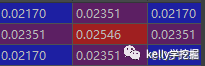
卷积核归一化后的各个位置取值（截图自pycharm的debug）：

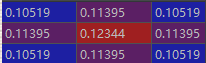
高斯卷积核的python代码：

def gaussian_kernel(self):
	kernel = np.zeros(shape=(self.kernel_size, self.kernel_size), dtype=np.float)
	radius = self.kernel_size//2
	for y in range(-radius, radius + 1):  # [-r, r]
		for x in range(-radius, radius + 1):
			# 二维高斯函数
			v = 1.0 / (2 * np.pi * self.sigma ** 2) * np.exp(-1.0 / (2 * self.sigma ** 2) * (x ** 2 + y ** 2))
			kernel[y + radius, x + radius] = v  # 高斯函数的x和y值 vs 高斯核的下标值
	kernel2 = kernel / np.sum(kernel)
	return kernel2

（2）如何在二维图像上进行卷积

对于二维矩阵，卷积时卷积核从左向右、从上而下的滑动，对应位置求加权和。一般图像是RGB三通道，需要逐个通道卷积，每个通道是一个二维矩阵。灰度图只有一个通道，直接卷积即可。

自行实现的二维离散卷积的python代码：

def my_conv2d(inputs: np.ndarray, kernel: np.ndarray):
    # 计算需要填充的行列数目，这里假定mode为“same”
    # 一般卷积核的hw都是奇数，这里实现方式也是基于奇数尺寸的卷积核
    h, w = inputs.shape
    kernel = kernel[::-1, ...][..., ::-1]  # 卷积的定义，必须旋转180度
    h1, w1 = kernel.shape
    h_pad = (h1 - 1) // 2
    w_pad = (w1 - 1) // 2
    inputs = np.pad(inputs, pad_width=[(h_pad, h_pad), (w_pad, w_pad)], mode="constant", constant_values=0)
    outputs = np.zeros(shape=(h, w))
    for i in range(h):  # 行号
        for j in range(w):  # 列号
            outputs[i, j] = np.sum(np.multiply(inputs[i: i + h1, j: j + w1], kernel))
    return outputs

scipy中已经提供二维卷积函数scipy.signal.convolve2d，可以直接调用，下图是和自行实现的对比效果。

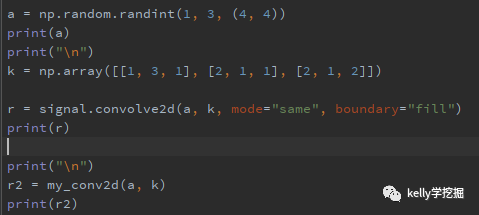
运行之后结果一致，验证自行实现的二维卷积正确。

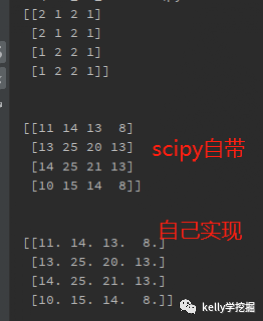
补充：scipy.signal.convolve2d的参数说明

in1：输入矩阵

in2：卷积核

mode：指示输出矩阵的尺寸，full代表完全离散线性卷积, valid代表输出尺寸等于输入尺寸-卷积核+1, same代表输出尺寸与输入尺寸一致。

boundary：需要填充时边界填充方式，fill代表使用常量值填充, wrap代表循环方式填充, symm代表以四周边为对称轴对称填充。

fillvalue：常量填充时的填充值

（四）完整代码和运行效果

完整的python代码​​​​​​

class GaussianBlur(object):
    def __init__(self, kernel_size=3, sigma=1.5):
        self.kernel_size = kernel_size
        self.sigma = sigma
        self.kernel = self.gaussian_kernel()

    def gaussian_kernel(self):
        kernel = np.zeros(shape=(self.kernel_size, self.kernel_size), dtype=np.float)
        radius = self.kernel_size//2
        for y in range(-radius, radius + 1):  # [-r, r]
            for x in range(-radius, radius + 1):
                # 二维高斯函数
                v = 1.0 / (2 * np.pi * self.sigma ** 2) * np.exp(-1.0 / (2 * self.sigma ** 2) * (x ** 2 + y ** 2))
                kernel[y + radius, x + radius] = v  # 高斯函数的x和y值 vs 高斯核的下标值
        kernel2 = kernel / np.sum(kernel)
        return kernel2

    def filter(self, img: Image.Image):
        img_arr = np.array(img)
        if len(img_arr.shape) == 2:
            new_arr = signal.convolve2d(img_arr, self.kernel, mode="same", boundary="symm")
        else:
            h, w, c = img_arr.shape
            new_arr = np.zeros(shape=(h, w, c), dtype=np.float)
            for i in range(c):
                new_arr[..., i] = signal.convolve2d(img_arr[..., i], self.kernel, mode="same", boundary="symm")
        new_arr = np.array(new_arr, dtype=np.uint8)
        return Image.fromarray(new_arr)

def main():
    img = Image.open("Jeep-cd.jpg").convert("RGB")
    img2 = GaussianBlur(sigma=2.5).filter(img)

    plt.subplot(1, 2, 1)
    plt.imshow(img)

    plt.subplot(1, 2, 2)
    plt.imshow(img2)

    # dpi参数维持图片的清晰度
    plt.savefig("gaussian.jpg", dpi=500)
    plt.show()
    pass

代码运行效果，发现经高斯模糊处理之后，图片发生明显模糊。

到此这篇关于python实现高斯模糊及原理详解的文章就介绍到这了,更多相关python 高斯模糊内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！