Python浮点数取整、格式化和NaN处理的操作方法

目录

• 1. 取整的三种方法
• 1.1 强转int类型
• 1.2 采用math.ceil和math.floor
• 1.3 采用round
• 2. 格式化浮点数输出
• 3. 执行精确的小数计算
• 4. 无穷大、负无穷大和NaN的判断测试
• 参考

强转int类型会直接对浮点数的小数部分进行截断（无论是正还是负）。还有一种方法是math.ceil和math.floor。无论是正数还是负数，都遵循：ceil往数轴正方向取整，floor往数轴负方向取整。round原型为round(value, ndigits)，可以将一个浮点数取整到固定的小数位。该函数对正数和负数都采取就近取整原则，而当某个值恰好等于两个整数间一半时，取整操作会取到离该值最近的那个偶数。

1. 取整的三种方法

1.1 强转int类型

这种方法会直接对浮点数的小数部分进行截断（无论是正还是负）。

print(int(2.7)) # 2
print(int(-2.7)) # -2

1.2 采用math.ceil和math.floor

这种方法的取整规则如下图所示：

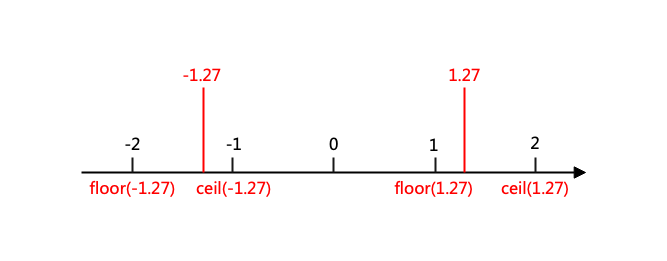
可以看到无论是正数还是负数，都遵循：ceil往数轴正方向取整，floor往数轴负方向取整。实例如下：

print(math.ceil(-1.27)) # -1
print(math.floor(-1.27)) # -2
print(math.ceil(1.27)) # 2
print(math.floor(1.27)) # 1

1.3 采用round

round原型为round(value, ndigits)，可以将一个浮点数取整到固定的小数位。该函数对正数和负数都采取就近取整原则，而当某个值恰好等于两个整数间一半时，取整操作会取到离该值最近的那个偶数。像1.5和2.5这样的值都会取整到2。示例如下：

print(round(1.23, 0)) # 1.0
print(round(1.23, 1)) # 1.2
print(round(1.27, 1)) # 1.3
print(round(-1.27, 1)) # -1.3
print(round(1.25361, 3)) # 1.254
print(round(1.5, 0)) # 2.0
print(round(2.5, 0)) # 2.0

传递给round()参数ndigits可以是负数，这种情况下回相应取整到十位、百位、千位：

a = 1627731
print(round(a, -1)) # 1627730
print(round(a, -2)) # 1627700
print(round(a, -3)) # 1628000

2. 格式化浮点数输出

注意对值输出时别把取整和格式化操作混为一谈。如果只是将数值以固定位数输出，一般是用不着round()的，只要在用format格式化时指定所需要的精度即可（format()格式化操作会根据round()的规则进行取整，最终返回一个字符串类型）。

x = 1234.56789
s = format(x, "0.2f")
print(type(s), format(x, "0.2f")) # <class 'str'> 1234.57

除了取整到固定小数位，format()还具有许多格式化功能，如格式化输出对齐，增加千分位分隔符等。实际上面的0.2f就表示至少对齐到0个字符（相当于没有对齐操作），并保留两位小数。

小提示：.2f也表示至少对齐到0个字符(默认是0)，并保留两位小数，
和0.2f二者是等效的。

更多示例如下：

# 往右调整以对齐到10个字符
print(format(x, ">10.1f")) #     1234.6
# 往右调整以对齐到10个字符
print(format(x, "<10.1f")) # 1234.6
# 居中以对齐到10个字符
print(format(x, "^10.1f")) #   1234.6
# 增加千位分隔符
print(format(x, ",")) # 1,234.56789
# 增加千位分隔符并保存到1位小数
print(format(x, "0,.1f")) # 1,234.6

如果想使用科学计数法，只要把f改成e或E即可：

print(format(x, "e")) # 1.234568e+03
print(format(x, "0.2E")) # 1.23E+03

此外，我们还可以利用字符串的translate()方法交换不同的分隔符：

swap_separators = {ord("."):",", ord(","):"."}
print(format(x, ",").translate(swap_separators)) # 1.234,56789

最后，我们这里提一下，调用字符串的.format()函数和单独调用format()函数可以达到相同的效果，如：

print("value is {:0.3f}".format(x)) # value is 1.235
print("The value is {:0,.2f}".format(x)) # The value is 1,234.57

当然我们也可以使用%操作符来对数值做格式化处理，如：

print("%.2f" % x)
print("%10.1f" % x)
print("%-10.1f" % x)

这种格式化操作虽然可行，但是比起更加现代化的format()方法，这种方法就显得不是那么强大了。如用%操作符来格式化数值时，有些功能就没法得到支持了（如添加千位分隔符）。

3. 执行精确的小数计算

我们在第一部分介绍了round()函数，我们有可能会企图用浮点取整的方式来“修正”精度上的问题，如：

a = 2.1
b = 4.2
c = a + b
print(c) # 6.300000000000001
print(c==6.3) # False
print(round(c, 2)) # 6.3 企图这样修正精度（？？？）

对大部分浮点数应用程序（包括科学计算与机器学习）来说，一般都不必（或者所不推荐）这么做。虽然Python的浮点运算会引入一些小误差，但这些误差实际上是底层CPU的浮点运算单元和IEEE 754浮点算数标准的一种“特性”。由于Python的浮点数类型保存的数据采用的是原始保存形式，因此只要代码中用到了float实例，那就无法避免这样的误差。

如果避免出现误差的行为非常重要（比如在金融应用中），那么可以考虑使用decimal模块。事实上在用Python做数据库库接口时经常碰到Decimal对象——当访问金融数据时尤其如此。我们通过使用Decimal对象解决上述问题：

from decimal import Decimal
a = Decimal('4.2')
b = Decimal('2.1')
print(type(a + b), a + b) # <class 'decimal.Decimal'> 6.3
print((a + b) == Decimal('6.3')) # True

这么做看起来似乎有点怪异（将数字以字符串的形式来指定）。但是Decimal对象能够以任何期望的方式来工作（支持所有常见的数学操作）。如果要将它们打印出来或者在字符串格式化函数中使用，它们看起来就和普通数字一样。它们也可以和普通int、float类型混合操作(最后会统一强转为Decimal类型)：

print(type(a + 1), a + 1) # <class 'decimal.Decimal'> 5.2

但是需要注意的是不要将其与普通float类型直接进行比较：

print((a + b) == 6.3) # False

decimal模块的强大之处在于在计算过程中灵活地控制数字的位数和四舍五入，如我们可以创建一个本地的上下文环境然后修改精度的设定，如：

from decimal import localcontext
a = Decimal("1.3")
b = Decimal("1.7")
print(a/b) # 0.7647058823529411764705882353
with localcontext() as ctx:
    ctx.prec = 3
    print(a/b) # 0.765 

with localcontext() as ctx:
    ctx.prec = 50
    print(a/b) # 0.764705882352941176470588235294117647058823529

不过还是我们上面所说的，如果我们处理的是科学或工程类型的问题，那么更常见的做法是直接使用普通的float浮点类型。首先，在真实世界中极少有东西需要计算到小数点后17位（float提供17位的精度），因此在计算中引入的微小误差不足挂齿；其次，原生的float浮点数运算性能要快许多——如果要执行大量计算，性能问题就显得很重要了。

在使用float类型时，我们同样还需要对类似相减抵消（substraction cancellation）以及把大数和小数加载一起的情况多加小心：

nums = [1.23e+18, 1, -1.23e+18]
print(sum(nums)) # 0.0

使用Decimal对象当然可以解决此问题。不过在不动用Decimal对象的情况下，我们可以使用math.fsum()以更精确的实现来解决：

import math
print(math.fsum(nums)) # 1.0

但对于其它复杂的数值算法，我们就需要研究算法本身，理解其误差传播(error propagation)了，这属于数值分析的研究范畴。在数值分析中数学家研究了大量数值算法，其中一些算法的误差处理能力优于其它算法，详情可以参见我的数值计算专栏《orion-orion：数值计算》，此处不再详述。

4. 无穷大、负无穷大和NaN的判断测试

在实际项目中我们需要对浮点数的无穷大、负无穷大或NaN（not a number）进行判断测试。在Python中没有特殊的语法来表示这些特殊的浮点值，但是它们可以通过float来创建：

a = float("inf")
b = float("-inf")
c = float("nan")
print(a, b, c) # inf -inf nan

要检查是否出现了这些值，可以使用math.isinf()和math.isnan()函数：

print(math.isinf(a)) # True
print(math.isnan(c)) # True

这些特殊浮点数的详细信息可以参考IEEE 754规范。但是我们这里有几个棘手的问题需要搞清楚，尤其是设计比较操作和操作符时可能出现的问题。

无穷大值在数学计算中会进行传播，如：

a = float("inf")
print(a + 45) # inf
print(a * 10) # inf
print(10/a) # 0.0

但是，某些关于无穷大值特定的操作会导致未定义的行为并产生NaN的结果，例如：

a = float("inf")
print(a/a) # nan
b = float("-inf")
print(a + b) # nan

NaN会通过所有的操作进行传播，且不会引发任何异常，如：

c = float("nan")
print(c + 23) # nan
print(c / 2) # nan
print(c + 2) # nan

有关NaN，一个微妙的特性是他们在做比较时从不会被判定为相等，如：

c = float("nan")
d = float("nan")
print(c == d) # False
print(c is d) # False

正因为如此，唯一安全检测NaN的方法是使用math.isnan()。

参考

[1] Martelli A, Ravenscroft A, Ascher D. Python cookbook[M]. " O'Reilly Media, Inc.", 2015.

[2] https://stackoverflow.com/questions/15765289/what-is-the-difference-between-0-2lf-and-2lf-as-printf-placeholders

[3] https://docs.python.org

到此这篇关于Python浮点数取整、格式化和NaN处理的操作方法的文章就介绍到这了,更多相关Python浮点数取整内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！