Java基础之二叉搜索树的基本操作

一、二叉搜索树插入元素

/**
 * user：ypc；
 * date：2021-05-18;
 * time: 15:09;
 */
     class Node {
        int val;
        Node left;
        Node right;

        Node(int val) {
            this.val = val;
        }
    }
    public void insert(int key) {
        Node node = new Node(key);
        if (this.root == null) {
            root = node;
        }
        Node cur = root;
        Node parent = null;
        while (cur != null) {
            if (cur.val == key) {
                //System.out.println("元素已经存在");
                return;
            } else if (cur.val > key) {
                parent = cur;
                cur = cur.left;
            } else {
                parent = cur;
                cur = cur.right;
            }
        }
        if (key > parent.val) {
            parent.right = node;
        } else {
            parent.left = node;
        }

    }

二、搜索指定节点

 public boolean search(int key) {
        Node cur = root;
        while (cur != null) {
            if (cur.val == key) {
                return true;
            } else if (cur.val > key) {
                cur = cur.left;
            } else {
                cur = cur.right;
            }
        }

        return false;
    }

三、删除节点方式一

 public void removenode1(Node parent, Node cur) {
        if (cur.left == null) {
            if (cur == root) {
                root = cur.right;
            } else if (cur == parent.right) {
                parent.left = cur.right;
            } else {
                parent.right = cur.right;
            }
        } else if (cur.right == null) {
            if (cur == root) {
                root.left = cur;
            } else if (cur == parent.right) {
                parent.right = cur.left;
            } else {
                parent.left = cur.left;
            }
        } else {
            Node tp = cur;
            Node t = cur.right;
            while (t.left != null) {
                tp = t;
                t = t.left;
            }
            if (tp.left == t) {
                cur.val = t.val;
                tp.left = t.right;
            }
            if (tp.right == t) {
                cur.val = t.val;
                tp.right = t.right;
            }
        }

    }

    public void remove(int key) {
        Node cur = root;
        Node parent = null;
        while (cur != null) {
            if (cur.val == key) {
                removenode1(parent, cur);
              //removenode2(parent, cur);
                return;
            } else if (key > cur.val) {
                parent = cur;
                cur = cur.right;
            } else {
                parent = cur;
                cur = cur.left;
            }
        }
    }

四、删除节点方式二

 public void removenode2(Node parent, Node cur) {

        if (cur.left == null) {
            if (cur == root) {
                root = cur.right;
            } else if (cur == parent.right) {
                parent.left = cur.right;
            } else {
                parent.right = cur.right;
            }
        } else if (cur.right == null) {
            if (cur == root) {
                root.left = cur;
            } else if (cur == parent.right) {
                parent.right = cur.left;
            } else {
                parent.left = cur.left;
            }
        } else {
            Node tp = cur;
            Node t = cur.left;
            while (t.right != null) {
                tp = t;
                t = t.right;
            }
            if (tp.right == t) {
                cur.val = t.val;
                tp.right = t.left;
            }
            if (tp.left == t) {
                cur.val = t.val;
                tp.left = t.left;
            }
        }

    }

五、运行结果

 /**
 * user：ypc；
 * date：2021-05-18;
 * time: 15:09;
 */
class TestBinarySearchTree {
    public static void main(String[] args) {
        int a[] = {5, 3, 4, 1, 7, 8, 2, 6, 0, 9};
        BinarySearchTree binarySearchTree = new BinarySearchTree();
        for (int i = 0; i < a.length; i++) {
            binarySearchTree.insert(a[i]);
        }
        binarySearchTree.inOrderTree(binarySearchTree.root);
        System.out.println();
        binarySearchTree.preOrderTree(binarySearchTree.root);
        binarySearchTree.remove(7);
        System.out.println();
        System.out.println("方法一删除后");
        binarySearchTree.inOrderTree(binarySearchTree.root);
        System.out.println();
        binarySearchTree.preOrderTree(binarySearchTree.root);
    }
}

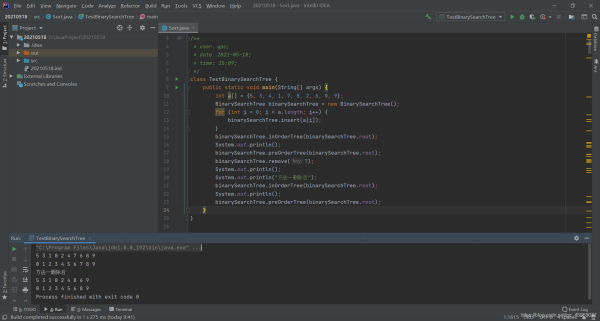
到此这篇关于Java基础之二叉搜索树的基本操作的文章就介绍到这了,更多相关二叉搜索树的基本操作内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！