Java用递归方法解决汉诺塔问题详解

目录
  • 前言
  • 一、问题描述
  • 二、问题分析
  • 三、解决方案
  • 四、示例

前言

博主之前有写过关于递归问题的思维模式：

递归的思路

下面将用这种思维模式来求解经典汉诺塔问题。

一、问题描述

汉诺塔（又称河内塔）问题是源于印度一个古老传说。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。

大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。

并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

问应该如何操作？

玩法如下：

1.有三根杆子A,B,C。A杆上有若干碟子

2.每次移动一块碟子,小的只能叠在大的上面

3.把所有碟子从A杆全部移到C杆上

二、问题分析

（两步直接解决问题）

1.第一步（先思考终止条件）

考虑n=1的情况：

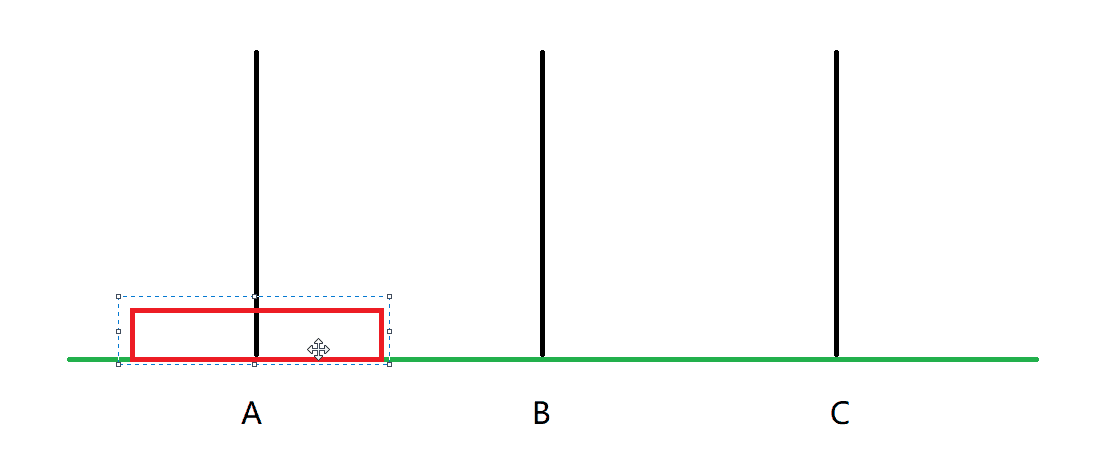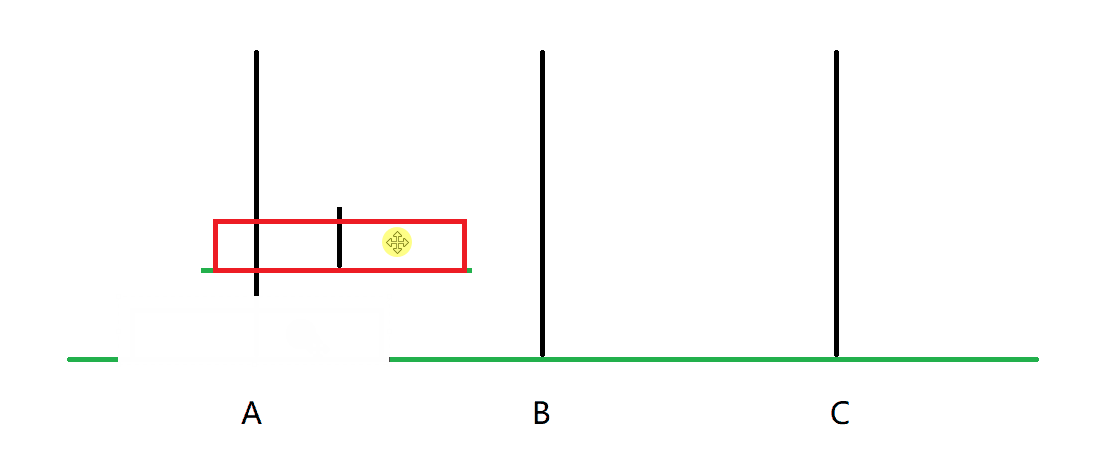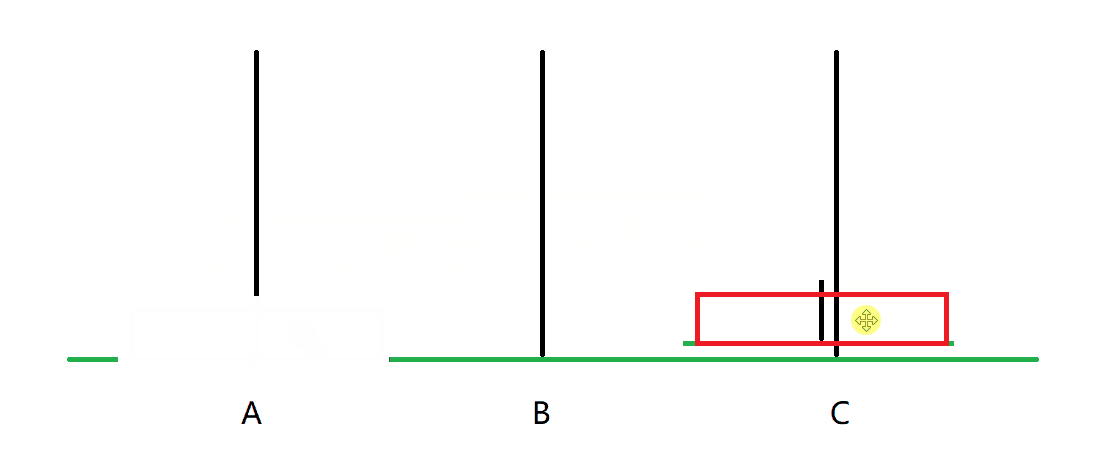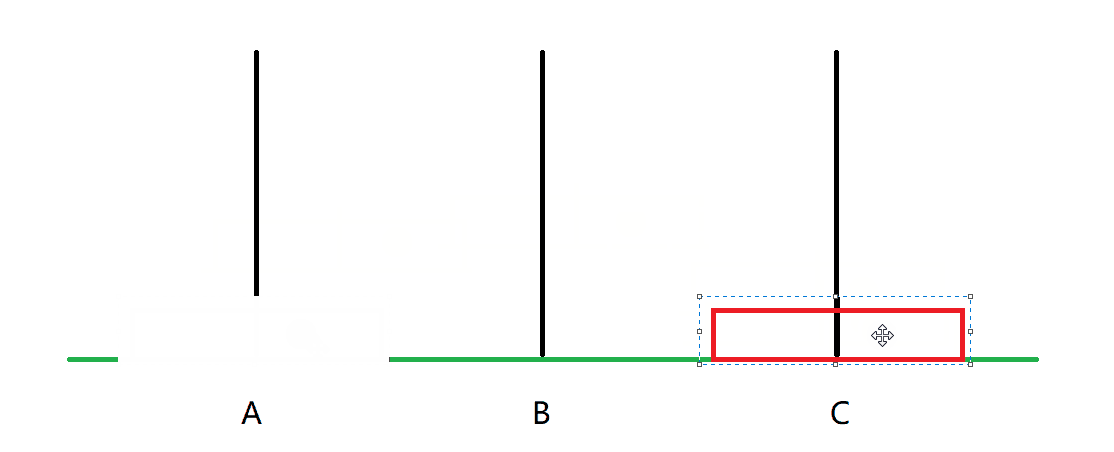
只需要把这个块从A移到C即可。

2.第二步（宏观看待整个问题）

当n>=2时，把如图蓝色框框想象成上面的n-1个块（我把它称为一堆块），红色框框表示的是最下面的一块（命名为底块），这样问题可以简化为如图所示的三步。

第一步：先把上面的一堆块 从A（起始柱子）移动到B（目标柱子）上，在这个过程中，C（辅助柱子）起到中转的作用（因为题目要求移动的过程中，小盘子要保证在大盘子上面）

第二步：把最下面的红色大块直接从A（起始柱子）移动到C（目标柱子）。这里注意，这一步的目标柱子和第一步的不一样。

第三步：把上面的一堆块从B（起始柱子）移动到C（目标柱子）上，A（辅助柱子）起到中转的作用。

三、解决方案

那么问题就很简单了，递归的代码就分为两部分：终止条件和递归逻辑。

上一篇博客讲到，我们思考递归问题的时候，可以直接把这个大问题拆解成很多个子问题，想象这个功能别人已经写好了（就是这个递归函数），我们做不到的功能直接调用这个递归函数就可以（注意逻辑）。

public class Recursion {
    public static void main(String[] args) {
        int n = 3;
        hanoiTower(n,'A','B','C');
    }

    /**
     * 传入n个盘子，编号从1..n，我就能按照汉诺塔的规则，从目标盘子A -> C ，B是辅助盘
     * @param nDisks
     * @param A 起始柱子
     * @param B 辅助柱子
     * @param C 目标柱子
     */
    public static void hanoiTower(int nDisks,char A,char B,char C) {
        // 边界
        if (nDisks == 1) {
            // 直接一步到位，用不到B，A上的这一个盘子从A -> C
            move(nDisks,A,C);
            return;
        }
        // n >= 2，核心步骤1,先把顶上的 n -1个小盘子从A -> B,C作为辅助
        hanoiTower(nDisks - 1,A,C,B);
        // 核心步骤2.此时A上就剩下第n个盘子，一步到位将最大的这个盘子一次移动到C
        move(nDisks,A,C);
        // 核心步骤3.此时再把B上的这n-1个盘子从B -> C,A作为辅助
        hanoiTower(nDisks - 1,B,A,C);
    }

    /**
     * 将编号为n的盘子从sourceTower移动到destTower
     * @param nDisks
     * @param sourceTower
     * @param destTower
     */
    public static void move(int nDisks, char sourceTower, char destTower) {
        System.out.println("编号为"+nDisks+"的盘子正在从"+sourceTower+"->"+destTower);
    }

四、示例

n=3的时候

以上就是用宏观思维去进行递归求解汉诺塔的方法，希望大家多多支持哟(●ˇ∀ˇ●)

到此这篇关于Java用递归方法解决汉诺塔问题详解的文章就介绍到这了,更多相关Java 汉诺塔内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！

赞 (0)

相关推荐

  • Java递归来实现汉诺塔游戏,注释详细

    Java递归来实现汉诺塔游戏,注释详细

    我们很容易能想到,可以用递归来实现汉诺塔游戏.因为要将n(n>1)个盘子从"源"柱子移到"目标"柱子,我们要先把n-1个盘子从"源"柱子移到"辅助"柱子上,然后把最底下那一个盘子移到目标柱子上,最后把"辅助柱"上的n-1个盘子移动到目标柱子上.n==1时直接移到目标柱上,也是递归的出口. 有了以上思路的铺垫,就可以开始实现代码了. public class HanoiDemo { public sta

  • Java基于栈方式解决汉诺塔问题实例【递归与非递归算法】

    Java基于栈方式解决汉诺塔问题实例【递归与非递归算法】

    本文实例讲述了Java基于栈方式解决汉诺塔问题.分享给大家供大家参考,具体如下: /** * 栈方式非递归汉诺塔 * @author zy * */ public class StackHanoi { /** * @param args */ public static void main(String[] args) { System.out.println("我们测试结果:"); System.out.println("递归方式:"); hanoiNormal(

  • java递归实现汉诺塔步骤介绍

    java递归实现汉诺塔步骤介绍

    汉诺塔的规则是:一共三根柱子,一根柱子从上到下套着有小到大的若干个圆盘,要将所有圆盘按照这个排放顺序移动到第三根柱子上,并且每次只能移动一个圆盘. 可以将整个过程分为三个步骤来看: 第一步:将除最大圆盘外的n-1个圆盘移动辅助柱子上 第二步:将最大的圆盘移动到目标柱子 第三步:将n-1个圆盘从辅助柱子移动到目标柱子 其中第一步又可以拆成一模一样的三步,可以看成一个n-1层的塔要移动到目标柱子,只不过目标柱子换了一个: 第三步也可以拆分成一模一样的三步: 多拆几次就会发现规律:第一步和第三步无论如

  • java基于递归算法实现汉诺塔问题实例

    本文实例讲述了java基于递归算法实现汉诺塔问题.分享给大家供大家参考,具体如下: package test; import java.util.List; import java.util.ArrayList; import java.util.Scanner; import sun.net.www.content.audio.x_aiff; /** * @author 年浩 * */ public class test { public static void move(char x,cha

  • Java编程用栈来求解汉诺塔问题的代码实例（非递归）

    [题目] 汉诺塔问题比较经典,这里修改一下游戏规则:现在限制不能从最左侧的塔直接移动到最右侧,也不能从最右侧直接移动到最左侧,而是必须经过中间.求当塔有N层的时候,打印最优移动过程和最优移动总步数. [解答] 上一篇用的是递归的方法解决这个问题,这里我们用栈来模拟汉诺塔的三个塔,也就是不用递归的方法 原理是这样的:修改后的汉诺塔问题不能让任何塔从左直接移动到右,也不能从右直接移动到左,而是要经过中间,也就是说,实际上能做的动作,只有四个:左->中,中->左,中->右,右->中 用栈

  • Java使用递归法解决汉诺塔问题的代码示例

    Java使用递归法解决汉诺塔问题的代码示例

    汉诺(Hanoi)塔问题:古代有一个梵塔,塔内有三个座A.B.C,A座上有n个盘子,盘子大小不等,大的在下,小的在上(如图). 有一个和尚想把这n个盘子从A座移到B座,但每次只能允许移动一个盘子,并且在移动过程中,3个座上的盘子始终保持大盘在下,小盘在上.在移动过程中可以利用B座,要求打印移动的步骤.如果只有一个盘子,则不需要利用B座,直接将盘子从A移动到C. 如果有2个盘子,可以先将盘子1上的盘子2移动到B:将盘子1移动到c:将盘子2移动到c.这说明了:可以借助B将2个盘子从A移动到C,当然,

  • java 汉诺塔Hanoi递归、非递归(仿系统递归)和非递归规律 实现代码

    程序如下: 复制代码 代码如下: View Code  /*  * Hanoi塔游戏 问题描述:  * 汉诺塔:汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具.  * 大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照  * 大小顺序摞着64片黄金圆盘.大梵天命令婆罗门把圆盘从下面开始按大小  * 顺序重新摆放在另一根柱子上.并且规定,在小圆盘上不能放大圆盘,在  * 三根柱子之间一次只能移动一个圆盘.  *   * fuction:实现 hanoi塔  *       

  • Java用递归方法解决汉诺塔问题详解

    Java用递归方法解决汉诺塔问题详解

    目录 前言 一.问题描述 二.问题分析 三.解决方案 四.示例 前言 博主之前有写过关于递归问题的思维模式: 递归的思路 下面将用这种思维模式来求解经典汉诺塔问题. 一.问题描述 汉诺塔(又称河内塔)问题是源于印度一个古老传说.大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘. 大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上. 并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘. 问应该如何操作? 玩法如下: 1.有三

  • C语言实现汉诺塔(图文详解)

    C语言实现汉诺塔(图文详解)

    目录 思路: 当n=1时: 当n=2时: 当n=3时: 当n=4时: 见代码 运行截图 总结 汉诺塔的游戏规则: 有三根金刚石柱子A.B.C,在A柱子上从下往上按照大小依次减小的顺序摞着64片黄金环.大梵天命令婆罗门把环从下面开始按大小顺序重新摆放在另一根柱子上.并且规定,在任何一个柱子上,小环上不能放大环,在三根柱子之间一次只能移动一个环. 即将A柱子上全部的环通过中间柱子B(B柱子作为中介)移动到C柱子上 当A只有一个环的时候: A->C 当A只有两个环的时候: A->B A->C

  • C++基于递归算法解决汉诺塔问题与树的遍历功能示例

    C++基于递归算法解决汉诺塔问题与树的遍历功能示例

    本文实例讲述了C++基于递归算法解决汉诺塔问题与树的遍历功能.分享给大家供大家参考,具体如下: 递归是把问题转化为规模缩小的同类问题,然后迭代调用函数(或过程)求得问题的解.递归函数就是直接或间接调用自身的函数. 递归两要素:递归关系和递归边界(终止条件),递归关系确定了迭代的层次结构,需要深入了解并分解问题:终止条件保证了程序的有穷性. 递归的应用有很多,常见的包括:阶乘运算.斐波那契数列.汉诺塔.数的遍历,还有大名鼎鼎的快排等等.理论上,递归问题都可以由多层循环来实现.递归的每次调用都会消耗

  • C#利用递归算法解决汉诺塔问题

    C#利用递归算法解决汉诺塔问题

    目录 一.什么是递归 二.汉诺塔问题 1.汉诺塔的故事 2.解决思路 3.怎么解决汉诺塔问题 4.具体代码实现 三.完整代码 一.什么是递归 方法调用自己的行为就是递归,递归必须要有终止条件,不然它会无限递归. 1.先来看一下一个递归的例子 此程序的Fact方法从大到小地一级一级地调用自己,直到参数为1,然后就开始返回一级一级的从小到大地累乘,然后就计算出number的阶乘了. static int Fact(int num) { if (num <= 1) { return num; } el

  • C#解决汉诺塔问题DEMO

    C#解决汉诺塔问题DEMO

    汉诺塔问题是学习递归的入门问题,这里用C#简单实现了一个汉诺塔之间传递盘子的小程序 通过简单绘图实现盘子在几个塔之间的转换: namespace 汉诺塔 { //盘子类 class HanioItem { public int HanoiItemHeight { get; set; }//盘子的高度 public int HanoiItemWidth { get; set; }//盘子的宽度 public Point HanoiItemPoint { get; set; }//画盘子的起始点 }

  • Java手把手必会的实例汉诺塔讲解练习

    Java手把手必会的实例汉诺塔讲解练习

    最适合菜鸟的汉诺塔讲解 问题引入 汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具.大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘.大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上.并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘. 让我们先从小事入手. 标记汉诺塔的三根柱子分别为 a ,b ,c 标记汉诺塔上的圆盘分别为:1 ,2,3,4 -n a 柱上面只有一个圆盘时 只有这一种走法 a柱上有两个圆盘时

随机推荐