C/C++最短路径算法之迪杰斯特拉Dijkstra的实现详解

目录

• 前言
• 一、迪杰斯特拉（Dijkstra）算法是什么
• 二、实现步骤
• 1.算法思路
• 2.进入主函数ShortestPath()
• 1.创建final数组并且初始化path[]、dist[]数组
• 2.对于节点的初始化
• 3.进入主循环
• 三、全部代码（邻接表下）
• 四、全部代码（邻接矩阵下）
• 五、测试代码（邻接表下）
• 总结

前言

我们在生活中常常面临对路径选择的决策问题，这就要用到最短路径的算法了。

对于我这种榆木脑袋，显然迪杰斯特拉的这种算法有点高深。主要是我笨。

对于网图来说，最短路径，就是指两个顶点之间经过的边上权值之和最小的路径，并且我们称路径上的第一个顶点就是源点，最后一个顶点式终点。

一、迪杰斯特拉（Dijkstra）算法是什么

迪杰斯特拉算法是一个按照路径长度递增的次序产生最短路径的算法。

二、实现步骤

1.算法思路

这里先采用邻接表来遍历。

在遍历节点时，找到未遍历节点中权值最小的进行遍历，并且及时更新最短路径长度dist数组[]。

首先设置path[]数组代表路径信息。 dist[] 表示最短路径长度。

int* path = (int*)malloc(sizeof(G.vexnum));
int* dist = (int*)malloc(sizeof(G.vexnum));

2.进入主函数ShortestPath()

1.创建final数组并且初始化path[]、dist[]数组

final数组来表示是否完成对该节点的最短路径求解。final[v]==1表示完成最短路径搜素，反之final[vi]==0表示未完成。

在算法中只有在求得最短路径后才会将final[vi]置为1，也可以简单理解为访问标志数组。

path数组全体初始化为0。

final数组因为最开始并没有完成最短路径求解，故置为0。

dist数组初始化为与vi相连的节点的权值，没连就是INFINITY（65535）。

int* final = (int*)malloc(sizeof(int) * g.vexnum);
	for (int i = 0; i < g.vexnum; i++) {
		path[i] = 0;
		final[i] = 0;
		dist[i] = INFNITY;
	}
	ArcNode* p = g.vertexlist[vi].firstarc;
	for (p; p != NULL; p = p->nextarc) {
		dist[p->adjvex] = p->weight;
	}

2.对于节点的初始化

在遍历vi节点时，vi到vi的路径为0，vi到vi之间也不需要求路径，故dist[vi]=0;final[vi]=1;

dist[vi] = 0;
final[vi] = 1;

肯定有人问，那path呢，path代表路径信息，vi时源点自然就是0了，当然初始化时也可以把path全初始化为-1，看个人习惯了。

3.进入主循环

将对刨掉源点的其他节点进行遍历，故外循环次数为g.vexnum-1次。

再在dist数组中找到权值最小并且未完成最短路径搜索的节点，用k来表示该节点下标。

其次找到最小权值k节点后，设置final[k]=1，再对k节点进行遍历，更新dist和path数组。

更新方法：若与k节点相连的节点未完成最短路径搜索并且k节点权值+该节点权值小于dist数组中的源点到该节点的最短路径，那么将更新dist数组中到该节点的最短路径，并且更新path数组，到该节点的前驱为k节点。

	int k;
	for (int v = 1; v < g.vexnum; v++) {
		int min = INFNITY;
		for (int w = 0; w < g.vexnum; w++) {
			if (!final[w] && dist[w] < min) {
				k = w;
				min = dist[w];
			}
		}
		final[k] = 1;
		ArcNode* p = g.vertexlist[k].firstarc;
		while (p != NULL) {
			if (!final[p->adjvex] && (p->weight + min) < dist[p->adjvex]) {
				dist[p->adjvex] = min + p->weight;
				path[p->adjvex] = k;
			}
			p = p->nextarc;
		}
	}

三、全部代码（邻接表下）

void ShortestPath(AdjList g, int vi, int* path, int* dist) {
	int* final = (int*)malloc(sizeof(int) * g.vexnum);
	for (int i = 0; i < g.vexnum; i++) {
		path[i] = 0;
		final[i] = 0;
		dist[i] = INFNITY;
	}
	ArcNode* p = g.vertexlist[vi].firstarc;
	for (p; p != NULL; p = p->nextarc) {
		dist[p->adjvex] = p->weight;
	}
	dist[vi] = 0;
	final[vi] = 1;
	int k;
	for (int v = 1; v < g.vexnum; v++) {
		int min = INFNITY;
		for (int w = 0; w < g.vexnum; w++) {
			if (!final[w] && dist[w] < min) {
				k = w;
				min = dist[w];
			}
		}
		final[k] = 1;
		ArcNode* p = g.vertexlist[k].firstarc;
		while (p != NULL) {
			if (!final[p->adjvex] && (p->weight + min) < dist[p->adjvex]) {
				dist[p->adjvex] = min + p->weight;
				path[p->adjvex] = k;
			}
			p = p->nextarc;
		}
	}
	free(final);
	return;
}

四、全部代码（邻接矩阵下）

思路大同小异，在初始化时有些不同，其他很相像。

void ShortestPath(AdjMatrix g, int vi, int* path, int* dist) {
	int* final = (int*)malloc(sizeof(int) * g.vexnum);
	for (int i = 0; i < g.vexnum; i++) {
		path[i] = 0;
		final[i] = 0;
		dist[i] = g.arc[vi][i];
	}
	dist[vi] = 0;
	final[vi] = 1;
	int k;
	for (int v = 1; v < g.vexnum; v++) {
		int min = INFNITY;
		for (int w = 0; w < g.vexnum; w++) {
			if (!final[w] && dist[w] < min) {
				k = w;
				min = dist[w];
			}
		}
		final[k] = 1;
		ArcNode* p = g.vertexlist[k].firstarc;
		for (int w = 0; w < g.vexnum; w++) {
			if (!final[w] && (min+g.arc[k][w])<dist[w]) {
				dist[w]=min+g.arc[k][w];
				path[w]=k;
			}
		}
	}
	free(final);
	return;
}

五、测试代码（邻接表下）

这里就测试一个邻接表下的。

自己花了个图

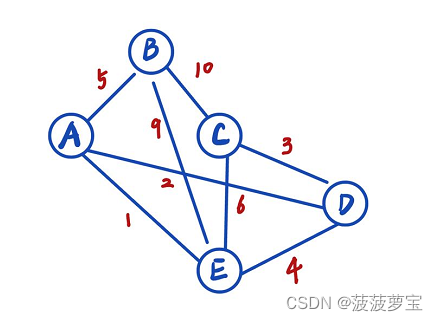
因为我的边表建立的时候A是第一个，自然A就是源点。

结果如下

很完美。

总结

很显然这个算法的时间复杂度是O(n²)，如果要知道任意顶点到其余所有顶点的最短路径，那么就可以对每一个顶点当作源点进行一次迪杰斯特拉算法。这时候后整个算法的时间复杂度也就成了O(n³)。这个和弗洛伊德算法的时间复杂度一样，但弗洛伊德算法那是相当的优雅。

到此这篇关于C/C++最短路径算法之迪杰斯特拉Dijkstra的实现详解的文章就介绍到这了,更多相关C/C++迪杰斯特拉内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！