Python深度学习pytorch神经网络块的网络之VGG

目录

• VGG块
• VGG网络
• 训练模型

与芯片设计中工程师从放置晶体管到逻辑元件再到逻辑块的过程类似，神经网络结构的设计也逐渐变得更加抽象。研究人员开始从单个神经元的角度思考问题，发展到整个层次，现在又转向模块，重复各层的模式。

使用块的想法首先出现在牛津大学的视觉几何组（visualgeometry Group）（VGG）的VGG网络中。通过使用循环和子程序，可以很容易地在任何现代深度学习框架的代码中实现这些重复的结构。

VGG块

经典卷积神经网络的基本组成部分是下面的这个序列：

1.带填充以保持分辨率的卷积层

2.非线性激活函数，如ReLU

3.汇聚层，如最大汇聚层

而一个VGG块与之类似，由一系列卷积层组成，后面再加上用于空间下采样的最大汇聚层。

在最初的VGG论文中，作者使用了带有 3 × 3卷积核、填充为1（保持高度和宽度）的卷积层，和带有 2 × 2 池化窗口、步幅为2（每个块后的分辨率减半）的最大汇聚层。

在下面的代码中，我们定义了一个名为vgg_block的函数来实现VGG块。

该函数有三个参数，分别对应于卷积层的数量num_convs、输入通道的数量in_channels和输出通道的数量out_channels。

import torch
from torch import nn
from d2l import torch as d2l

def vgg_block(num_convs, in_channels, out_channels):
	layers = []
	for _ in range(num_convs):
		layers.append(nn.Conv2d(in_channels, out_channels, kernel_size = 3, padding=1))
		leyers.append(nn.ReLU())
		in_channels = out_channels
	layers.append(nn.MaxPool2d(kernel_size=2, stride=2))
	return nn.Sequential(*layers)

VGG网络

与AlexNet、LeNet一样，VGG网络可以分为两个部分：第一部分主要由卷积层和汇聚层组成，第二部分由全连接层组成。如下图所示：

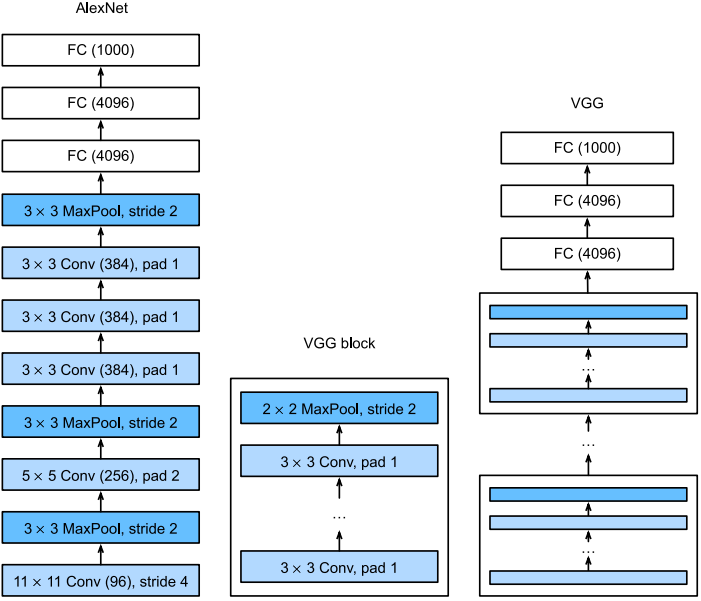
VGG神经网络连续连接上图的几个VGG块（在vgg_block函数中定义）。其中有超参数变量conv_arch。该变量指定了每个VGG块里的卷积层的个数和输出通道数。全连接模块则与AlexNet中的相同。

原始VGG网络中有5个卷积块，其中前两个块各有一个卷积层，后三个块包含两个卷积层。第一个模块有64个输出通道，每个后续模块将输出通道数量翻倍，直到数字达到512。由于该网络使用8个卷积层和3个全连接层，因此它通常被称为VGG-11。

conv_arch = ((1, 64), (1, 128), (2, 256), (2, 512), (2, 512))

下面的代码实现了VGG-11。可以通过在conv_arch上执行for循环来简单实现。

def vgg(conv_arch):
	conv_blks = []
	in_channels = 1
	# 卷积层部分
	for (num_convs, out_channels) in conv_arch:
		conv_blks.append(vgg_block(num_convs, in_cannels, out_channels))
		in_channels = out_channels

	return nn.Sequential(
		*conv_blks, nn.Flatten(),
		# 全连接层部分
		nn.Linear(out_channels * 7 * 7, 4096), nn.ReLU(), nn.Dropout(0.5),
		nn.Linear(4096, 4096), nn.ReLU(), nn.Dropout(0.5),
		nn.Linear(4096, 10)
	)

net = vgg(conv_arch)

接下来，我们将构建一个高度和宽度为224的单通道数据样本，以观察每个层输出的形状。

X = torch.randn(size=(1, 1, 224, 224))
for blk in net:
	X = blk(X)
	print(blk.__class__.__name__, 'output shape: \t', X.shape)

Sequential output shape: torch.Size([1, 64, 112, 112])
Sequential output shape: torch.Size([1, 128, 56, 56])
Sequential output shape: torch.Size([1, 256, 28, 28])
Sequential output shape: torch.Size([1, 512, 14, 14])
Sequential output shape: torch.Size([1, 512, 7, 7])
Flatten output shape: torch.Size([1, 25088])
Linear output shape: torch.Size([1, 4096])
ReLU output shape: torch.Size([1, 4096])
Dropout output shape: torch.Size([1, 4096])
Linear output shape: torch.Size([1, 4096])
ReLU output shape: torch.Size([1, 4096])
Dropout output shape: torch.Size([1, 4096])
Linear output shape: torch.Size([1, 10])

我们在每个块的高度和宽度减半，最终高度和宽度都为7。最后再展平表示，送入全连接层处理。

训练模型

由于VGG-11比AlexNet计算量更大，因此我们构建了一个通道数较少的网络，足够用于训练Fashion-MNIST数据集。

ratio = 4
small_conv_arch = [(pair[0], pair[1] // ratio) for pair in conv_arch]
net = vgg(small_conv_arch)

除了使用略高的学习率外，模型训练过程与AlexNet类似。

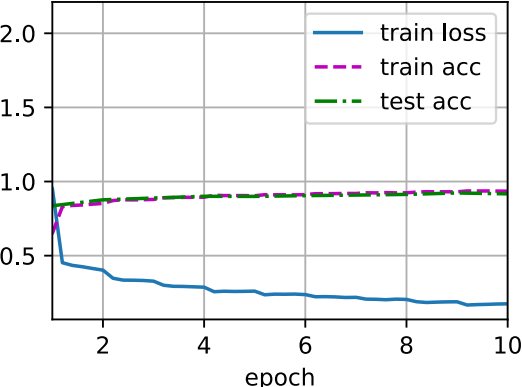
lr, num_epochs, batch_size = 0.05, 10, 128

train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

loss 0.175, train axx 0.935, test acc 0.917
2559.6 examples/sec on cuda:0

以上就是Python神经网络块的网络之VGG深度学习的详细内容，更多关于Python神经网络VGG块的网络的资料请关注我们其它相关文章！