python 一维二维插值实例

一维插值

插值不同于拟合。插值函数经过样本点，拟合函数一般基于最小二乘法尽量靠近所有样本点穿过。常见插值方法有拉格朗日插值法、分段插值法、样条插值法。

拉格朗日插值多项式：当节点数n较大时，拉格朗日插值多项式的次数较高，可能出现不一致的收敛情况，而且计算复杂。随着样点增加，高次插值会带来误差的震动现象称为龙格现象。

分段插值：虽然收敛，但光滑性较差。

样条插值:样条插值是使用一种名为样条的特殊分段多项式进行插值的形式。由于样条插值可以使用低阶多项式样条实现较小的插值误差，这样就避免了使用高阶多项式所出现的龙格现象，所以样条插值得到了流行。

在CODE上查看代码片派生到我的代码片

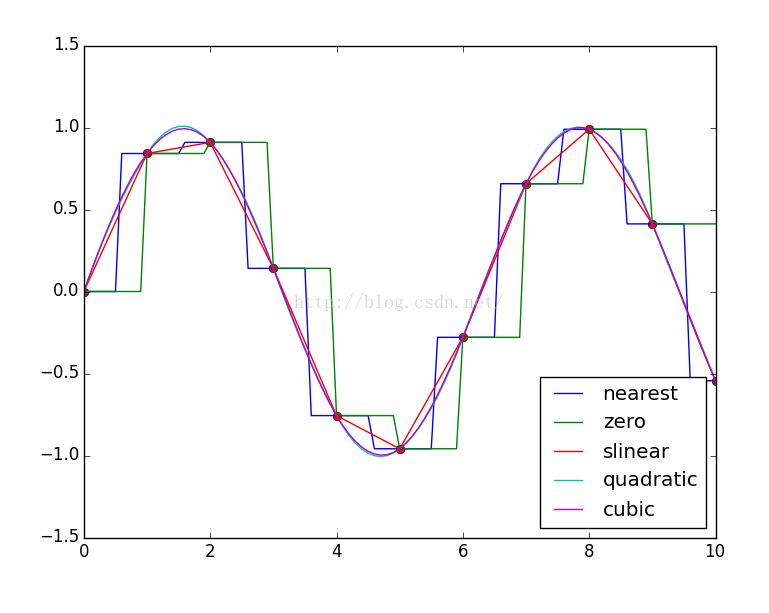
#!/usr/bin/env python
# -*-coding:utf-8 -*-
import numpy as np
from scipy import interpolate
import pylab as pl 

x=np.linspace(0,10,11)
#x=[ 0. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.]
y=np.sin(x)
xnew=np.linspace(0,10,101)
pl.plot(x,y,"ro") 

for kind in ["nearest","zero","slinear","quadratic","cubic"]:#插值方式
 #"nearest","zero"为阶梯插值
 #slinear 线性插值
 #"quadratic","cubic" 为2阶、3阶B样条曲线插值
 f=interpolate.interp1d(x,y,kind=kind)
 # ‘slinear', ‘quadratic' and ‘cubic' refer to a spline interpolation of first, second or third order)
 ynew=f(xnew)
 pl.plot(xnew,ynew,label=str(kind))
pl.legend(loc="lower right")
pl.show() 

结果:

二维插值

方法与一维数据插值类似，为二维样条插值。

在CODE上查看代码片派生到我的代码片

# -*- coding: utf-8 -*-
"""
演示二维插值。
"""
import numpy as np
from scipy import interpolate
import pylab as pl
import matplotlib as mpl 

def func(x, y):
 return (x+y)*np.exp(-5.0*(x**2 + y**2)) 

# X-Y轴分为15*15的网格
y,x= np.mgrid[-1:1:15j, -1:1:15j] 

fvals = func(x,y) # 计算每个网格点上的函数值 15*15的值
print len(fvals[0]) 

#三次样条二维插值
newfunc = interpolate.interp2d(x, y, fvals, kind='cubic') 

# 计算100*100的网格上的插值
xnew = np.linspace(-1,1,100)#x
ynew = np.linspace(-1,1,100)#y
fnew = newfunc(xnew, ynew)#仅仅是y值 100*100的值 

# 绘图
# 为了更明显地比较插值前后的区别，使用关键字参数interpolation='nearest'
# 关闭imshow()内置的插值运算。
pl.subplot(121)
im1=pl.imshow(fvals, extent=[-1,1,-1,1], cmap=mpl.cm.hot, interpolation='nearest', origin="lower")#pl.cm.jet
#extent=[-1,1,-1,1]为x,y范围 favals为
pl.colorbar(im1) 

pl.subplot(122)
im2=pl.imshow(fnew, extent=[-1,1,-1,1], cmap=mpl.cm.hot, interpolation='nearest', origin="lower")
pl.colorbar(im2) 

pl.show() 

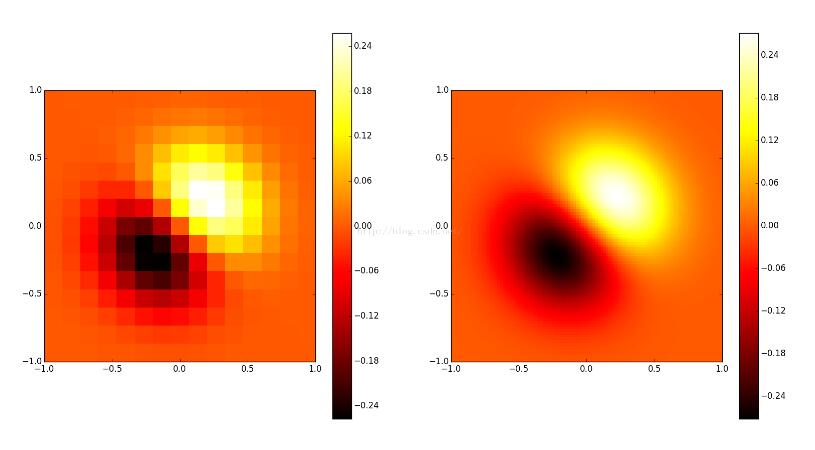
左图为原始数据，右图为二维插值结果图。

二维插值的三维展示方法

在CODE上查看代码片派生到我的代码片

# -*- coding: utf-8 -*-
"""
演示二维插值。
"""
# -*- coding: utf-8 -*-
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
import matplotlib as mpl
from scipy import interpolate
import matplotlib.cm as cm
import matplotlib.pyplot as plt 

def func(x, y):
 return (x+y)*np.exp(-5.0*(x**2 + y**2)) 

# X-Y轴分为20*20的网格
x = np.linspace(-1, 1, 20)
y = np.linspace(-1,1,20)
x, y = np.meshgrid(x, y)#20*20的网格数据 

fvals = func(x,y) # 计算每个网格点上的函数值 15*15的值 

fig = plt.figure(figsize=(9, 6))
#Draw sub-graph1
ax=plt.subplot(1, 2, 1,projection = '3d')
surf = ax.plot_surface(x, y, fvals, rstride=2, cstride=2, cmap=cm.coolwarm,linewidth=0.5, antialiased=True)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('f(x, y)')
plt.colorbar(surf, shrink=0.5, aspect=5)#标注 

#二维插值
newfunc = interpolate.interp2d(x, y, fvals, kind='cubic')#newfunc为一个函数 

# 计算100*100的网格上的插值
xnew = np.linspace(-1,1,100)#x
ynew = np.linspace(-1,1,100)#y
fnew = newfunc(xnew, ynew)#仅仅是y值 100*100的值 np.shape(fnew) is 100*100
xnew, ynew = np.meshgrid(xnew, ynew)
ax2=plt.subplot(1, 2, 2,projection = '3d')
surf2 = ax2.plot_surface(xnew, ynew, fnew, rstride=2, cstride=2, cmap=cm.coolwarm,linewidth=0.5, antialiased=True)
ax2.set_xlabel('xnew')
ax2.set_ylabel('ynew')
ax2.set_zlabel('fnew(x, y)')
plt.colorbar(surf2, shrink=0.5, aspect=5)#标注 

plt.show() 

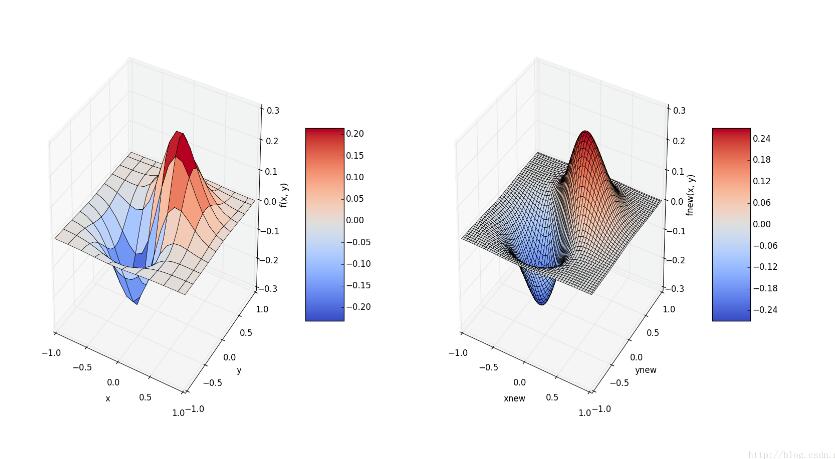
左图的二维数据集的函数值由于样本较少，会显得粗糙。而右图对二维样本数据进行三次样条插值，拟合得到更多数据点的样本值，绘图后图像明显光滑多了。

补充知识：python中对Dataframe二维查表插值的实现方法

今天在计算风力发电机捕捉风能功率的时候，需要对叶片扫略面积内的风能做个功率效率折减，即Cp系数，Cp的定义如下，即实际利用的风能与输入风能的比例

输入风能是空气密度与风速的函数，可以直接计算：

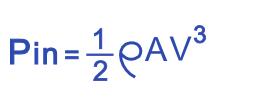
那么实际得到的能力是Pin与Cp的乘积。

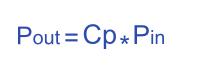
Cp通常是一个二维表，横坐标是TSR(叶尖速与风速的比值)，纵坐标是PITCH Angle（桨叶角）。风机的运行数据中是包含风速 ，转速以及桨叶角信息的，并且通过直接读入到DataFrame，那么就需要根据TSR与PA对Cp查表并且插值得到Cp。主要用到scipy.interpolate.interp2d创建插值函数并查表，另外Dataframe不能直接用插值函数，这里做了个for循环分行插值查表。

from scipy.interpolate import interp2d
df_rotormap = pd.read_csv('filepath',header = None) #读取Cp表
x = np.array(df_rotormap.iloc[:,0].dropna()) #Cp表的X坐标是TSR
y = np.array(df_rotormap.iloc[:,1]) #Cp表的Y坐标是pitch angle
z = np.array(df_rotormap.iloc[:,2:]) #Cp表的具体值，y行x列

rho = 1.225 #kg/m3
s = (141/2)**2*np.pi #m2
df_cal['TSR'] = df_cal['发电机转速（PDM1）']/148*141*np.pi/60/df_cal['风速']

func_new = interp2d(x,y,z,kind = 'linear') #定义二维表插值函数，选择线性插值

cp_list = []
for i in range(df_cal.shape[0]):
 cp = float(func_new(df_cal['TSR'][i],df_cal['1号桨叶角度'][i])) #输入X,Y坐标， 输出插值计算的Cp
 cp_list.append(cp)

df_cal['cp'] = cp_list #把Cp放回到Dataframe中去

df_cal['air_power'] = 0.5*rho*s*df_cal['风速']**3*df_cal['cp']

以上这篇python 一维二维插值实例就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持我们。