R语言与多元线性回归分析计算案例

目录
  • 计算实例
  • 分析
  • 模型的进一步分析

计算实例

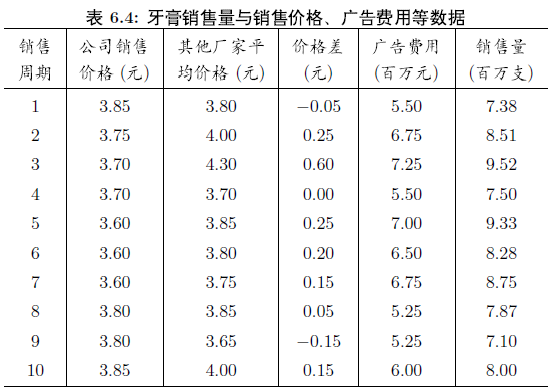
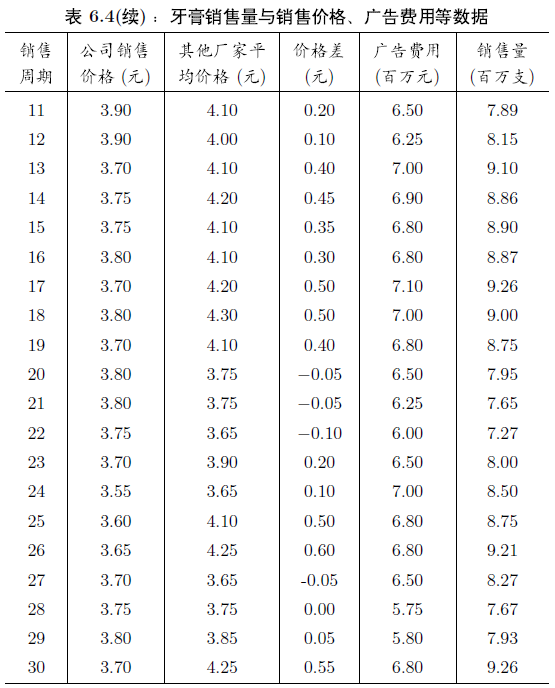
例 6.9 某大型牙膏制造企业为了更好地拓展产品市场，有效地管理库存，公司董事会要求销售部门根据市场调查，找出公司生产的牙膏销售量与销售价格，广告投入等之间的关系，从而预测出在不同价格和广告费用下销售量。为此，销售部门的研究人员收集了过去30个销售周期（每个销售周期为4周）公司生产的牙膏的销售量、销售价格、投入的广告费用，以及周期其他厂家生产同类牙膏的市场平均销售价格，如表6.4所示。

试根据这些数据建立一个数学模型，分析牙膏销售量与其他因素的关系，为制订价格策略和广告投入策略提供数量依据。

分析

由于牙膏是生活的必需品，对于大多数顾客来说，在购买同类牙膏时，更多的会关心不同品牌之间的价格差，而不是它们的价格本身。因此，在研究各个因素对销售量的影响时，用价格差代替公司销售价格和其他厂家平均价格更为合适。

模型的建立与求解

记牙膏销售量为Y，价格差为X1，公司的广告费为X2，假设基本模型为线性模型:

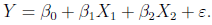
输入数据，调用R软件中的lm（）函数求解，并用summary（）显示计算结果（程序名：exam0609.R）

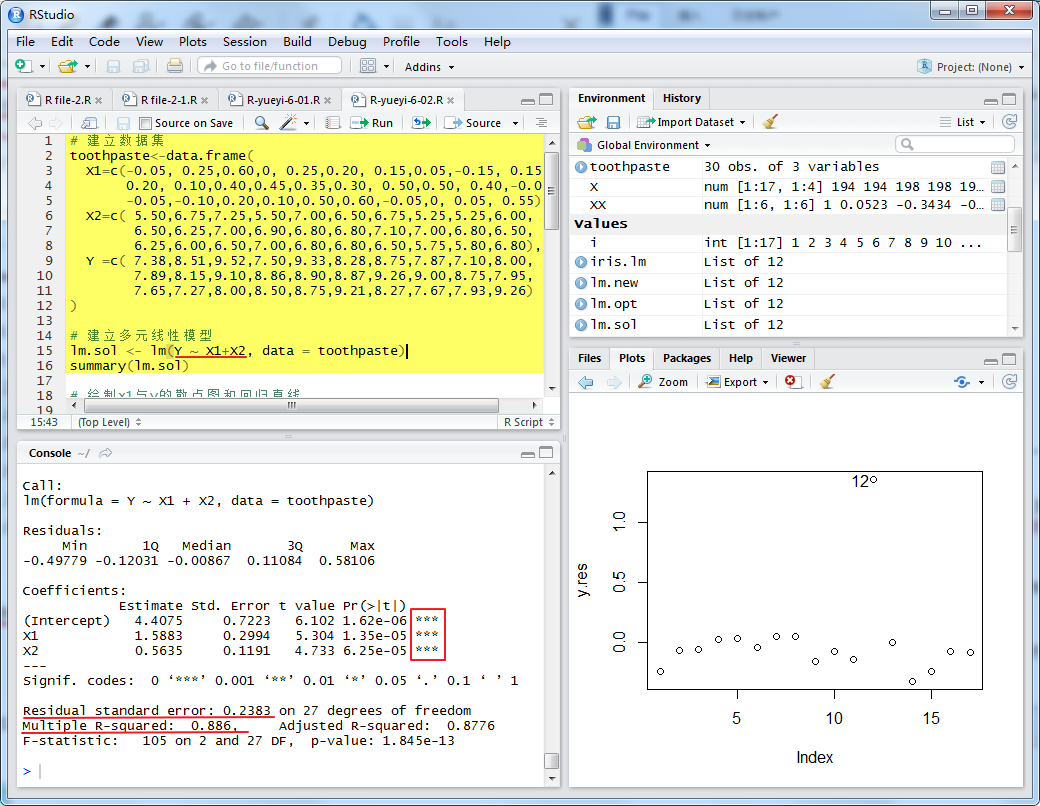
计算结果通过线性回归系数检验和回归方程检验，由此得到销售量与价格差与广告费之间的关系为：

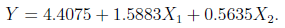
模型的进一步分析

为进一步分析回归模型，我们画出y与x1和y与x2散点图。从散点图上可以看出，对于y与x1，用直线拟合较好。而对于y与x2，则用二次曲线拟合较好，如下图：

绘制x1与y的散点图和回归直线

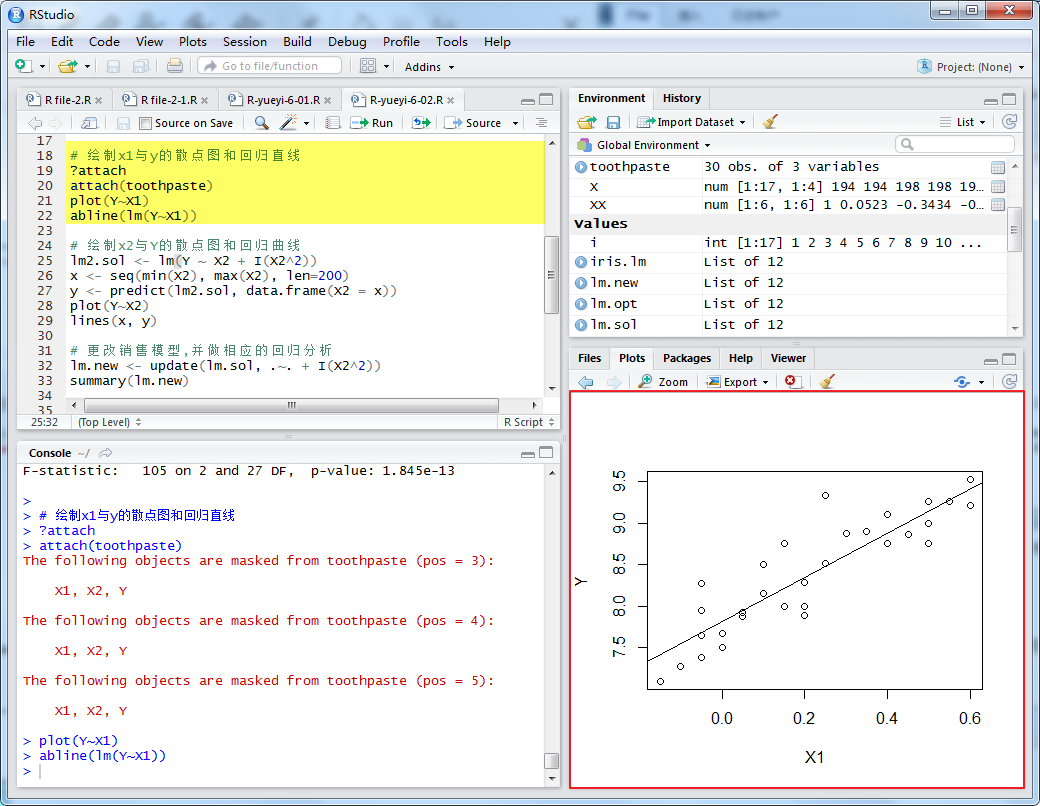
绘制x2与y的散点图和回归曲线

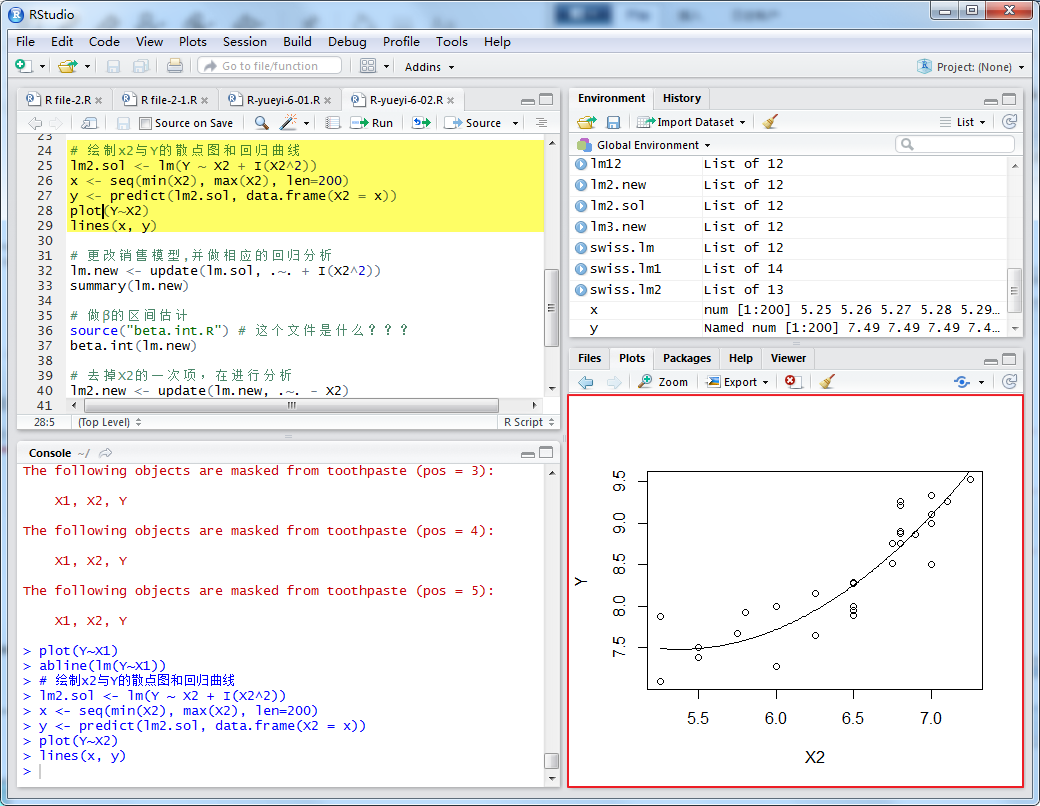
其中 I(X2^2)，表示模型中X2的平方项，及X22，从上图中，将销售量模型改为：

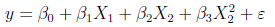
似乎更合理，我们做相应的回归分析：

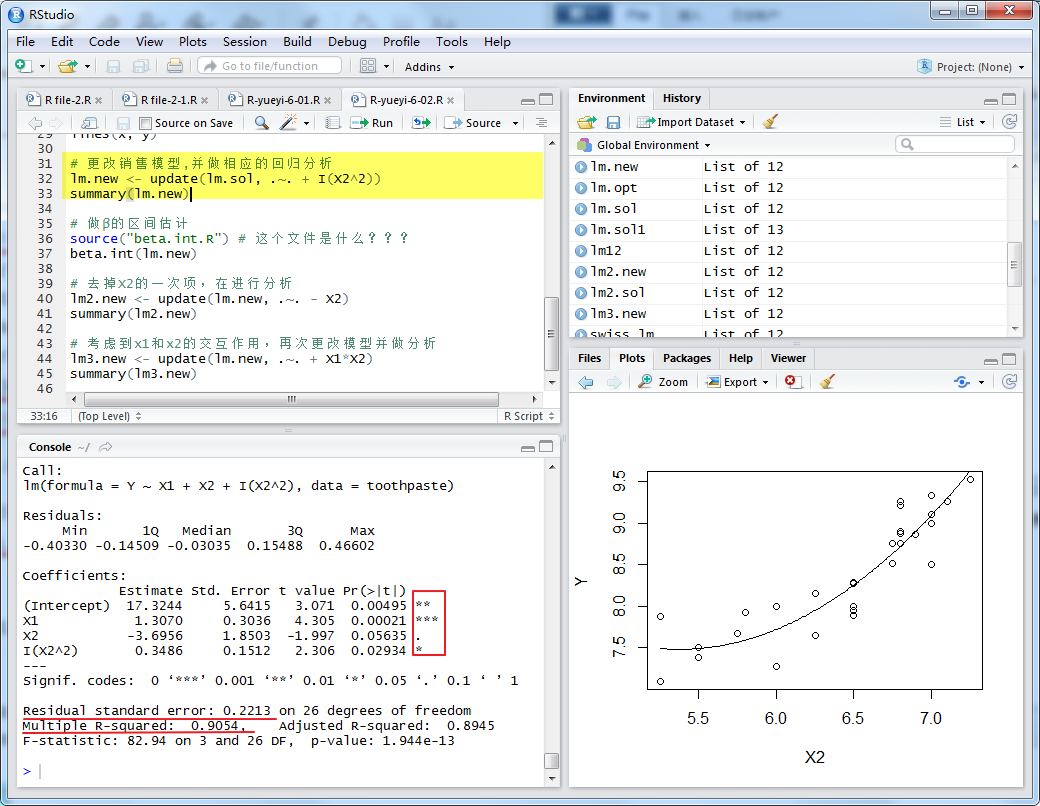
此时，我们发现，模型残差的标准差Residual standard error有所下降，相关系数的平方Multiple R-squared有所上升，这说明模型修正的是合理的。但同时也出现了一个问题，就是对于β2的P-值>0.05。为进一步分析，做β的区间估计。

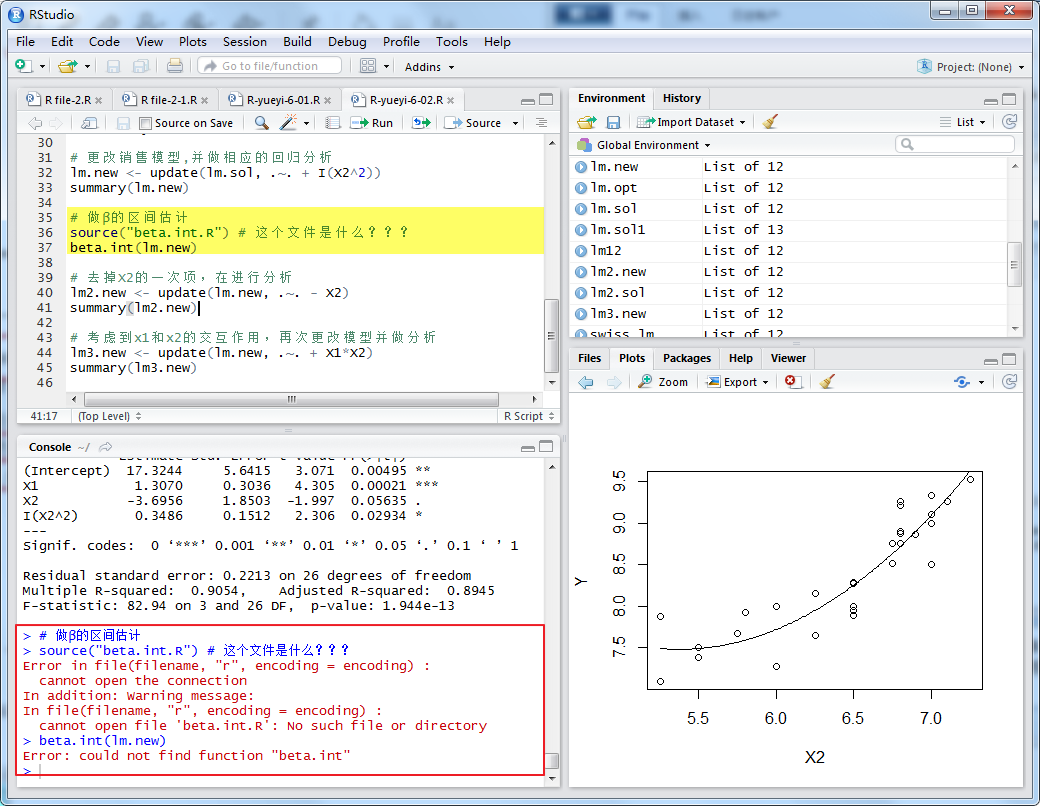
如上错误出现？？？？！！！！直接引用结果如下：

β2的区间估计为[ –7.49886317, 0.1076898 ]，它包含了0，也就是说，β2的值可能为0. 因此，去掉X2的一次项，在进行分析：

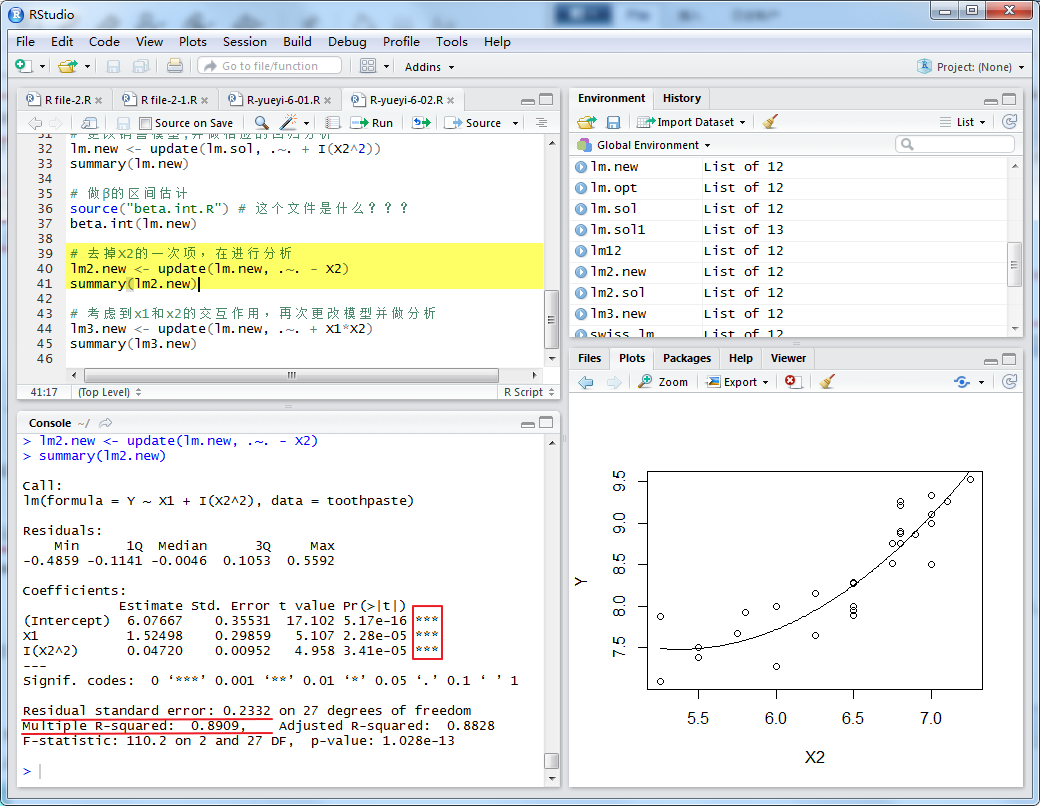
此模型虽然通过了F检验和T检验，但与上一模型对比来看，Residual standard error上升，Multiple R-squared下降。这又是此模型的不足之处。

在做进一步的修正，考虑X1和X2交互作用，及模型为：

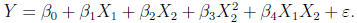
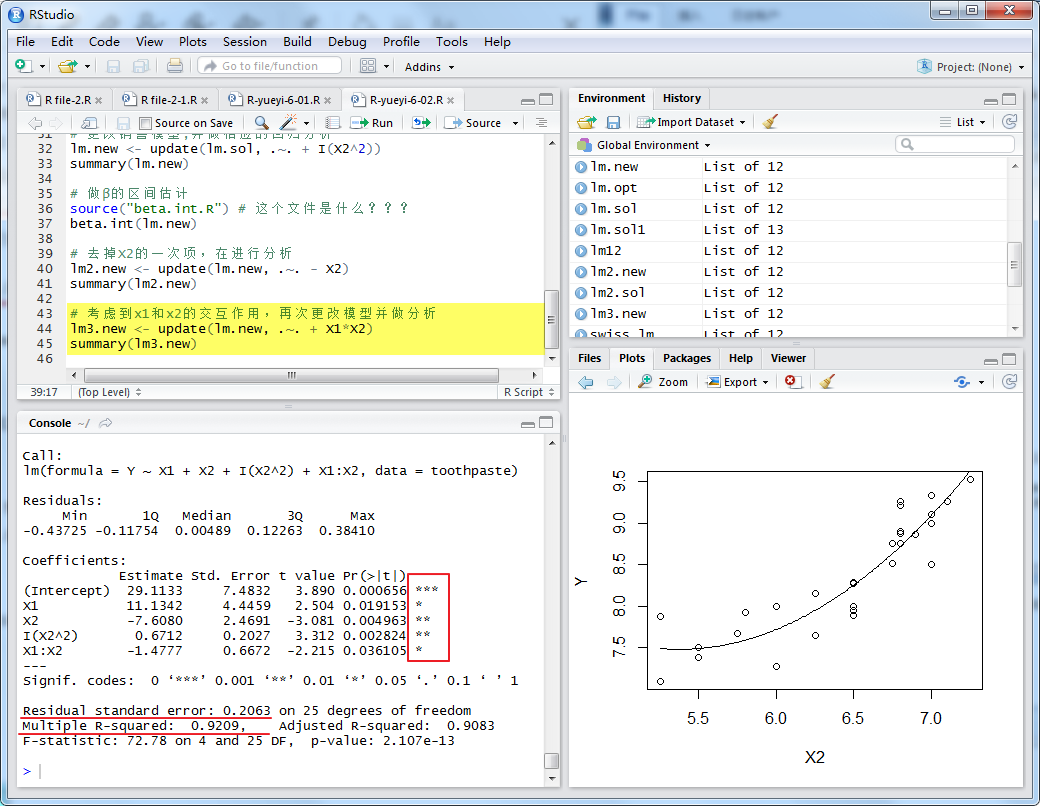
模型通过T检验和F检验，并且Residual standard error减少，Multiple R-squared增加。因此，最终模型选为：

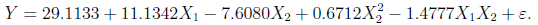
到此这篇关于R语言与多元线性回归分析计算案例的文章就介绍到这了,更多相关R语言与多元线性回归内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！

赞 (0)

相关推荐

  • R语言如何实现多元线性回归

    R语言如何实现多元线性回归

    R小白几天的摸索 红色为输入,蓝色为输出 输入数据 先把数据用excel保存为csv格式放在"我的文档"文件夹 打开R软件,不用新建,直接写 回归计算 求三个平方和 置信区间(95%) 散点图(最显著的因变量) 拟合图 一元线性回归 结果:(看图) 变量系数  Estimate 变量系数标准误  Std. Error T检验值  t value T检验p值  Pr(>|t|) 均方根误差  Residual standard error 判定系数  R-squared 调整判定系

  • R语言与多元线性回归分析计算案例

    R语言与多元线性回归分析计算案例

    目录 计算实例 分析 模型的进一步分析 计算实例 例 6.9 某大型牙膏制造企业为了更好地拓展产品市场,有效地管理库存,公司董事会要求销售部门根据市场调查,找出公司生产的牙膏销售量与销售价格,广告投入等之间的关系,从而预测出在不同价格和广告费用下销售量.为此,销售部门的研究人员收集了过去30个销售周期(每个销售周期为4周)公司生产的牙膏的销售量.销售价格.投入的广告费用,以及周期其他厂家生产同类牙膏的市场平均销售价格,如表6.4所示. 试根据这些数据建立一个数学模型,分析牙膏销售量与其他因素的关

  • 关于多元线性回归分析——Python&SPSS

    原始数据在这里 1.观察数据 首先,用Pandas打开数据,并进行观察. import numpy import pandas as pd import matplotlib.pyplot as plt %matplotlib inline data = pd.read_csv('Folds5x2_pp.csv') data.head() 会看到数据如下所示: 这份数据代表了一个循环发电厂,每个数据有5列,分别是:AT(温度), V(压力), AP(湿度), RH(压强), PE(输出电力).我

  • R语言实现线性回归的示例

    R语言实现线性回归的示例

    在统计学中,线性回归(Linear Regression)是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析. 简单对来说就是用来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法. 回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析.如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析. 一元线性回归分析法的数学方程: y = ax + b

  • R语言实现支持向量机SVM应用案例

    R语言实现支持向量机SVM应用案例

    IRIS数据集简介 IRIS数据集中的数据源于1936年费希尔法发表的一篇论文.彼时他收集了三种鸢尾花(分别标记为setosa.versicolor和virginical)的花萼和花瓣数据.包括花萼的长度和宽度,以及花瓣的长度和宽度.我们将根据这四个特征来建立支持向量机模型从而实现对三种鸢尾花的分类判别任务. 有关数据可以从datasets软件包中的iris数据集里获取,下面我们演示性地列出了前5行数据.成功载入数据后,易见其中共包含了150个样本(被标记为setosa.versicolor和v

  • R语言多元线性回归实例详解

    R语言多元线性回归实例详解

    目录 一.模型简介 二.求解过程 总结 一.模型简介 一元线性回归是一个主要影响因素作为自变量来解释因变量的变化,在现实问题研究中,因变量的变化往往受几个重要因素的影响,此时就需要用两个或两个以上的影响因素作为自变量来解释因变量的变化,这就是多元回归亦称多重回归.当多个自变量与因变量之间是线性关系时,所进行的回归分析就是多元线性回归. 二.求解过程 这里我使用的数据是包里面自带的数据,我们导入并进行查看: 可以看到第一列是我们的数据标签(无数学含义),后面五列分别为对应的五个特征即相应的数值.我

  • R语言多元Logistic逻辑回归应用实例

    R语言多元Logistic逻辑回归应用实例

    可以使用逐步过程确定多元逻辑回归.此函数选择模型以最小化AIC. 如何进行多元逻辑回归 可以使用阶梯函数通过逐步过程确定多元逻辑回归.此函数选择模型以最小化AIC. 通常建议不要盲目地遵循逐步程序,而是要使用拟合统计(AIC,AICc,BIC)比较模型,或者根据生物学或科学上合理的可用变量建立模型. 多元相关是研究潜在自变量之间关系的一种工具.例如,如果两个独立变量彼此相关,可能在最终模型中都不需要这两个变量,但可能有理由选择一个变量而不是另一个变量. 多元相关 创建数值变量的数据框 Data.

  • R语言-计算频数和频率的操作

    首先,筛选出需要的列: data <- data2[,which(colnames(data2) %in% c("产品分类", "期数", "逾期月数"))] 产品分类 期数 逾期月数 委托贷款 24 1 委托贷款 36 1 担保贷款 24 2 委托贷款 24 2 信用贷款 36 4 担保贷款 24 3 信用贷款 24 1 委托贷款 36 3 担保贷款 24 2 现在希望得到每种产品种类在不同期数时 逾期月数的占比,使用table函数: #

  • R语言-计算平均值不同函数的区别说明

    函数mean > mean(x) > num x1 x2 x3 10378050.50 89.45 81.18 80.45 此时对编号也求了平均值,不过往往我们只想对后面的数据求平均值.而且此时会出现一个警告.因为x是一个数据框,不是数值,所以不能直接用mean()函数. 函数colMeans() > colMeans(x) num x1 x2 x3 10378050.50 89.45 81.18 80.45 > colMeans(x)[c("x1","

  • R语言科学计算RcppArmadillo简明手册

    R语言科学计算RcppArmadillo简明手册

    目录 1. 常用数据类型 2. 数学运算 3. 向量.矩阵和域的创建 基本创建 用函数创建 4. 初始化,元素访问,属性和成员函数 4.1. 元素初始化 Element initialization 4.2. 元素访问 Element access 4.3. 子矩阵访问 Submatrix view 矩阵X的连续子集访问 向量V的连续子集访问 向量或矩阵X的间断子集访问 立方体(三维矩阵)Q 的切片 slice 域F的子集访问 4.4. 属性 Attribute 4.5. 其他成员函数 Othe

随机推荐