利用C++求解八数码问题实例代码

目录

• 问题描述：
• 内容提要：
• 实验步骤：
• 实验步骤
• 分析说明（包括核心代码及解释）
• 总结心得

问题描述：

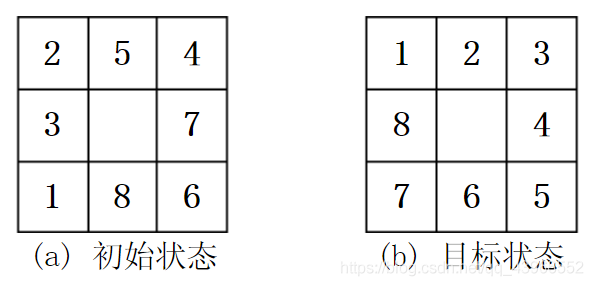
八数码，在3×3的方格棋盘上，摆放着1到8这八个数码，有1个方格是空的，其初始状态如图1所示，要求对空格执行空格左移、空格右移、空格上移和空格下移这四个操作使得棋盘从初始状态到目标状态。（注：图片给的例子无解。）

内容提要：

分别用广度优先搜索策略、深度优先搜索策略和启发式搜索算法（至少两种）求解八数码问题；分析估价函数对启发式搜索算法的影响；探究讨论各个搜索算法的特点。

实验步骤：

1.随机生成一个八数码问题分布，设计一个可解的目标状态（要求棋盘9个位置都不同）。

2.分别用广度优先搜索策略、深度优先搜索策略和至少两种启发式搜索算法求解八数码问题。

实验步骤

1.广度优先搜索

先从空白格周围开始搜索，上下左右四个方向找到了可交换的位置，就把位置交换之后的状态放入队列中，再从队列中取出队头元素，重复以上步骤。

2.有界深度搜索

先设定一个搜索的界限值，从空白格的四周开始搜索，找到了可交换的位置，就把该状态放进栈中，交换位置之后继续搜索，直到搜索到了界限值并且四周都搜索完毕没有可交换的位置，该状态出栈，取出栈顶元素继续重复以上步骤搜索。

3.启发式搜索

从空白格的四周开始搜索，把空白格放进open表中，从open表中取出表头，找出该层中上下左右四个方向搜索到可交换的位置，放进close表中，并计算出该状态与目标状态不同的格子数为id值，找出该层中最小id值的状态，再把这些状态放入open表中，重复上述步骤。

4.启发式搜索A*

先构造一个优先级队列，从空白格四周开始搜索，把空白格放入open表中，并计算出该状态的id值即层数加该状态不同格子与移动到目标状态最小位移数，取出open表中表头元素放进close表，搜索可以交换的位置放进open，重复该步骤。

分析说明（包括核心代码及解释）

1.广度优先搜索

#include<iostream>
#include<map>
#include<queue>
#include<stack>
using namespace std;

queue<int>Q;
map<int, int>vis;     //记录该状态是否被访问过
map<int, int>step;      //记录层数
map<int,int>parent;     //记录该状态的上一个状态
stack<int>out;
int dis[4][2] = { -1,0,0,1,1,0,0,-1 };     //左、上、右、下
int u, v;

int change(int** p, int a, int b)   //把数组矩阵转为一串数字
{
	int t = 0;
	for (int i = 0; i < a; i++)
		for (int j = 0; j < b; j++)
			t = t * 10 + p[i][j];
	return t;
}

int bfs(int** p, int a, int b)    //广度搜索
{
	int x, y, uu;    //x,y--空格所在的行列号，uu--队头八字码状态
	Q.push(u);     //把初始状态放入队列
	vis[u] = 1;      //被访问过标记为1
	step[u] = 0;      //初始层数为0
	while (Q.size())       //队空搜索结束
	{
		uu = u = Q.front();
		Q.pop();
		if (u == v)
			return step[v];
		for(int i=a-1;i>=0;i--)       //把八字码状态的数字转为数组
			for (int j = b - 1; j >= 0; j--)
			{
				p[i][j] = uu % 10, uu = uu / 10;
				if (p[i][j] == 0)     //标记空格位置
					x = i, y = j;
			}
		for (int i = 0; i < 4; i++)     //空格四周搜索
		{
			int nu;
			if (!(x == 0 && i == 0) && !(y == b - 1 && i == 1) && !(x == a - 1 && i == 2) && !(y == 0 && i == 3))   //当空格所走位置合理
			{
				p[x][y] = p[x + dis[i][0]][y + dis[i][1]], p[x + dis[i][0]][y + dis[i][1]] = 0;     //交换空格位置
				nu = change(p, a, b);
				if (!vis[nu])      //若该状态没有被访问过
				{
					Q.push(nu);      //入队
					vis[nu] = 1;
					step[nu] = step[u] + 1;     //层数在上一个状态层数上加一
					parent[nu] = u;          //记录该状态的父状态
				}
				p[x + dis[i][0]][y + dis[i][1]] = p[x][y], p[x][y] = 0;      //还原空格位置继续搜索
			}
		}
	}
	return -1;
}

int main()
{
	cout << "广度搜索" << endl;
	int m, n, s, t;
	int** mau, ** mav;
	cout << "输入m*n；" << endl;
	cin >> m >> n;
	mau = new int* [n], mav = new int* [n];
	for (int i = 0; i < n; i++)
		mau[i] = new int[m], mav[i] = new int[m];
	cout << "初始状态:" << endl;
	for (int i = 0; i < m; i++)
		for (int j = 0; j < n; j++)
			cin >> mau[i][j];
	cout << "最终状态:" << endl;
	for (int i = 0; i < m; i++)
		for (int j = 0; j < n; j++)
			cin >> mav[i][j];
	u = change(mau, m, n), v = change(mav, m, n);
	s = bfs(mau, m, n);
	if (s != -1)       //返回层数
	{
		cout << "到达目标状态需要 " << s << " 步" << endl;
		t = v;
		while (t)        //把所有的父状态入栈
		{
			out.push(t);
			t = parent[t];
		}
		while (out.size())      //输出目标状态的八字码求解过程
		{
			int** o;
			t = out.top();
			out.pop();
			o = new int* [n];
			for (int i = 0; i < n; i++)
				o[i] = new int[m];
			for (int i = m - 1; i >= 0; i--)
				for (int j = n - 1; j >= 0; j--)
					o[i][j] = t % 10, t /= 10;
			for (int i = 0; i < m; i++)
			{
				for (int j = 0; j < n; j++)
					cout << o[i][j] << " ";
				cout << endl;
			}
			cout << "======" << endl;
		}
	}
	else cout << "无解" << endl;     //没有返回层数
}

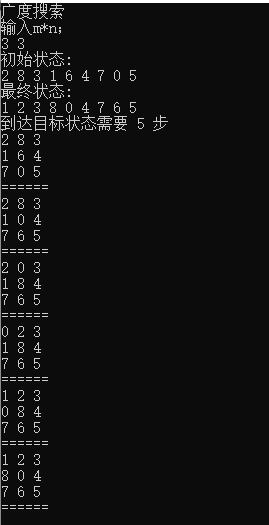
实验结果：

2.有界深度搜索

#include<iostream>
#include<queue>
#include<stack>
#include<map>
using namespace std;

int m, n, k;
map<int,int>vis;     //记录是否被访问
map<int, int>step;     //记录层数
map<int, int>d;      //记录访问方向
map<int, int>parent;      //记录该状态的上一个状态
stack<int>zhan;
stack<int>out;
int fx[4][2] = { 0,-1,-1,0,0,1,1,0 };      //左，上，右，下
int change(int** q)    //将数组转为数字
{
	int s=0;
	for (int i = 0; i < m; i++)
		for (int j = 0; j < n; j++)
			s = s * 10 + q[i][j];
	return s;
}

int dfs(int u,int v)     //有界深度搜索
{
	int now, find;         //now--现在的八字码状态，find--移动空格之后的八字码状态
	int** p;
	zhan.push(u);     //先把初始状态放进栈里
	vis[u] = 1;        //访问过的状态标记为1
	step[u] = 0;       //初始层数为0
	p = new int* [n];
	for (int i = 0; i < n; i++)
		p[i] = new int[m];
	while (zhan.size())      //栈空即搜索结束
	{
		int s, x0, y0, x=-1, y=-1;   //x0，y0--空格所在的行号、列号；x,y--空格移动后所在的行号、列号
		s = now = zhan.top();
		if (now == v)          //找到目标状态，返回层数
			return step[v];
		d[now]++;
		for(int i=m-1;i>=0;i--)      //把八字码状态的数字转换为数组
			for (int j = n-1; j >=0; j--)
			{
				p[i][j] = s % 10;
				s = s / 10;
				if (p[i][j] == 0)      //标记空格所在位置
					x0 = i, y0 = j;
			}
		switch (d[now])       //根据记录的方向次数移动空格位置
		{
		case 1: x = x0 + fx[0][0], y = y0 + fx[0][1]; break;   //左
		case 2: x = x0 + fx[1][0], y = y0 + fx[1][1]; break;   //上
		case 3: x = x0 + fx[2][0], y = y0 + fx[2][1]; break;   //右
		case 4: x = x0 + fx[3][0], y = y0 + fx[3][1]; break;   //下
		}
		if (x >= 0 && x < m && y >= 0 && y < n)      //当空格移动的位置合理
		{
			p[x0][y0] = p[x][y], p[x][y] = 0;      //交换位置
			find = change(p);
			if (!vis[find])          //若该八字码状态没有被访问过
			{
				zhan.push(find);      //将该状态压入栈
				vis[find] = 1;
				step[find] = step[now] + 1;       //层数在上一曾基础上加一
				parent[find] = now;
				if (find == v)
					return step[v];
			}
	    }
		if (d[now] > 4||step[find]==k-1)     //若该状态所有方向搜索完毕或者已经到达了深搜的界限，该状态值出栈
			zhan.pop();
	}
	return -1;
}

int main()
{
	cout << "有界深度搜索" << endl;
	int u, v, t;
	int** mau, ** mav;      //初始八字码状态、目标八字码状态
	cout << "输入m*n：" << endl;
	cin >> m >> n;
	cout << "输入界：" << endl;
	cin >> k;
	mau = new int* [n];
	mav = new int* [n];
	for (int i = 0; i < n; i++)
		mau[i] = new int[m], mav[i] = new int[m];
	cout << "输入初始状态：" << endl;
	for (int i = 0; i < m; i++)
		for (int j = 0; j < n; j++)
			cin >> mau[i][j];
	cout << "输入最终状态：" << endl;
	for (int i = 0; i < m; i++)
		for (int j = 0; j < n; j++)
			cin >> mav[i][j];
	u = change(mau), v = change(mav);
	if (dfs(u, v) >= 0)     //返回了正确的层数
	{
		cout << "到达目标状态需要 " << dfs(u, v) << " 步：" << endl;
		t = v;
		while (t)    //把该状态的父状态压入栈
		{
			out.push(t);
			t = parent[t];
		}
		while (out.size())     //输出栈中八字码求解状态过程
		{
			int** o;
			t = out.top();
			out.pop();
			o = new int* [n];
			for (int i = 0; i < n; i++)
				o[i] = new int[m];
			for (int i = m - 1; i >= 0; i--)
				for (int j = n - 1; j >= 0; j--)
					o[i][j] = t % 10, t /= 10;
			for (int i = 0; i < m; i++)
			{
				for (int j = 0; j < n; j++)
					cout << o[i][j] << " ";
				cout << endl;
			}
			cout << "======" << endl;
		}
	}
	else cout << "无解" << endl;    //没有返回层数
}

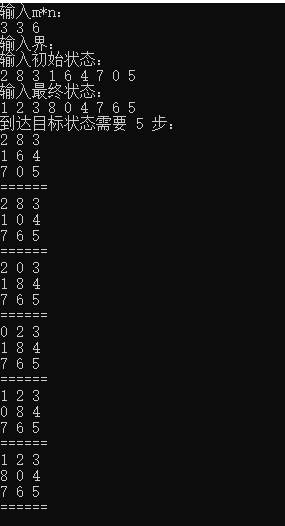
实验结果：

3.启发式搜索

#include<iostream>
#include<queue>
#include<map>
#include<stack>
using namespace std;

map<int, int>vis;
map<int, int>step;
map<int, int>id;
map<int, int>parent;
queue<int>open;
queue<int>close;
queue<int>nclose;
stack<int>out;
int m, n;
int dir[4][2] = { 0,-1,-1,0,0,1,1,0 };     //左、上、右、下

int change(int**p)    //把数组转为数字
{
	int s = 0;
	for(int i=0;i<m;i++)
		for (int j = 0; j < n; j++)
			s = s * 10 + p[i][j];
	return s;
}

void getid(int a,int b)      //获取与目标状态不同的格子数
{
	int c;
	c = a;
	for (int i = 0; i < m * m; i++)
	{
		if ((a % 10) != (b % 10))
			id[c]++;
		a = a / 10, b = b / 10;
	}
}

int A (int u,int v)      //启发式搜索
{
	open.push(u);     //把初始状态放进open表中
	vis[u] = 1;      //标记该状态已被访问
	getid(u, v);      //获取该状态与目标状态不同的格子数
	while (open.size())      //open表为空结束搜索
	{
		int q, p, w, x, y, newx, newy, size;
		if (open.front() == v)     //找到目标状态
			return step[v];
		size = open.size();
		for(int i=0;i<size;i++)     //找出该层数中，最小的id值
		{
			int** r;
			w=q=open.front();    //取出表头元素
			open.pop();
			r = new int* [n];
			for (int i = 0; i < n; i++)
				r[i] = new int[m];
			for (int i = m - 1; i >= 0; i--)       //找到空白格位置
				for (int j = n - 1; j >= 0; j--)
				{
					r[i][j] = q % 10, q = q / 10;
					if (r[i][j] == 0)
					{
						x = i, y = j;        //标记空白格位置
					}
				}
			for (int i = 0; i < 4; i++)     //搜索该状态的四个方向
			{
				newx = x + dir[i][0], newy = y + dir[i][1];
				if (newx >= 0 && newx < m && newy >= 0 && newy < n)    //若该位置可交换
				{
					r[x][y] = r[newx][newy];     //交换空白格位置
					r[newx][newy] = 0;
					p = change(r);
					if (!vis[p])     //该状态没有被访问过
					{
						close.push(p);      //把该状态放进close表
						nclose.push(p);
						vis[p] = 1;
						step[p] = step[w] + 1;     //层数在原来状态上加一
						parent[p] = w;     //标记父状态
						getid(p, v);
					}
					r[newx][newy] = r[x][y];     //变回原来状态
					r[x][y] = 0;
				}
			}
		}
		if (close.size())    //若close表不为空
		{
			int csize = close.size(), min;
			min = id[nclose.front()];
			for (int i = 0; i < csize; i++)      //找出close表中id的最小值
				if (id[nclose.front()] < min)
				{
					min = id[nclose.front()];
					nclose.pop();
				}
				else nclose.pop();
			for (int i = 0; i < csize; i++)      //把close表中id最小值的状态放进open表中
				if (id[close.front()] == min)
				{
					open.push(close.front());
					close.pop();
				}
				else close.pop();
		}
	}
	return -1;
}

int main()
{
	cout << "A搜索" << endl;
	int u, v, t;
	int** mau, ** mav;
	cout << "输入m*n：" << endl;
	cin >> m >> n;
	mau = new int* [n], mav = new int* [n];
	for (int i = 0; i < n; i++)
		mau[i] = new int[m], mav[i] = new int[m];
	cout << "输入初始状态：" << endl;
	for (int i = 0; i < m; i++)
		for (int j = 0; j < n; j++)
			cin >> mau[i][j];
	cout << "输入最终状态：" << endl;
	for (int i = 0; i < m; i++)
		for (int j = 0; j < n; j++)
			cin >> mav[i][j];
	u = change(mau), v = change(mav);
	if (A(u, v) != -1)
	{
		cout << "到达目标状态需要 " << A(u, v) << " 步" << endl;
		t = v;
		while (t)
		{
			out.push(t);
			t = parent[t];
		}
		while (out.size())    //输出到达目标状态的过程
		{
			int** o;
			t = out.top();
			out.pop();
			o = new int* [n];
			for (int i = 0; i < n; i++)
				o[i] = new int[m];
			for (int i = m - 1; i >= 0; i--)
				for (int j = n - 1; j >= 0; j--)
					o[i][j] = t % 10, t /= 10;
			for (int i = 0; i < m; i++)
			{
				for (int j = 0; j < n; j++)
					cout << o[i][j] << " ";
				cout << endl;
			}
			cout << "======" << endl;
		}

	}
	else cout << "无解" << endl;
}

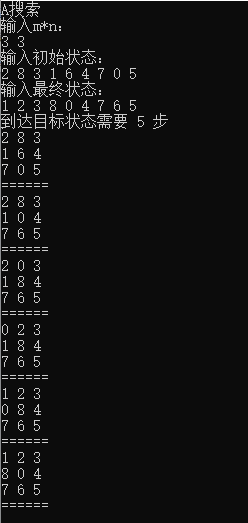
实验结果：

4.启发式搜索A*

#include<iostream>
#include<queue>
#include<stack>
#include<map>
using namespace std;

int m, n;
int dir[4][2] = { 0,-1,-1,0,0,1,1,0 };     //左、上、右、下

struct A
{
	int data;
	int id;
	friend bool operator < (A a,A b)    //按照id值小的方案构造优先级队列
	{
		return a.id > b.id;
	}
};

priority_queue<A>open;
queue<A>close;
stack<int>out;
map<int, int>vis;
map<int, int>step;
map<int, int>parent;

int change(int **q)    //把数组转为数字
{
	int s=0;
	for (int i = 0; i < m; i++)
		for (int j = 0; j < n; j++)
			s = s * 10 + q[i][j];
	return s;
}

void getid(A &u,A v)     //获取id值
{
	int** q, ** w;
	int a, b, s=0;
	a = u.data, b = v.data;
	q = new int* [n], w = new int* [n];
	for (int i = 0; i < n; i++)
		q[i] = new int[m], w[i] = new int[m];
	for(int i=m-1;i>=0;i--)
		for (int j = n-1; j >=0; j--)
		{
			q[i][j] = a % 10, w[i][j] = b % 10;
			a = a / 10, b = b / 10;
		}
	for(int i=0;i<m;i++)         //该状态不同的格子数移动到目标状态所需要的最小位移数
		for(int j=0;j<n;j++)
			if (q[i][j] != 0 && q[i][j] != w[i][j])
				for (int k = 0; k < m; k++)
					for (int l = 0; l < n; l++)
						if (q[i][j] == w[k][l])
							s = s + abs(k - i) + abs(l - j);
	s = s + step[u.data];      //加上层数
	u.id = s;
}

int Aplus(A u,A v)
{
	vis[u.data] = 1;   //标记初始状态已被访问过
	step[u.data] = 0;     //初始层数为0
	getid(u, v);
	open.push(u);     //把初始状态放入open表中
	while (open.size())
	{
		int q, nq, x, y, newx, newy;
		int** w;
		w = new int* [n];
		for (int i = 0; i < n; i++)
			w[i] = new int[m];
		close.push(open.top());    //把要搜索的状态放入close表中
		open.pop();
		nq = q = close.front().data;
		if (close.front().data == v.data)     //找到目标状态
			return step[v.data];
		for (int i = m-1; i >=0; i--)      //找到空白格位置
			for (int j = n-1; j >=0; j--)
			{
				w[i][j] = nq % 10, nq /= 10;
				if (w[i][j] == 0)      //标记空白格位置
					x = i, y = j;
			}
		for (int i = 0; i < 4; i++)        //搜索四个方向
		{
			A z;
			int e;
			newx = x + dir[i][0], newy = y + dir[i][1];
			if (newx >= 0 && newx < m && newy >= 0 && newy < n)     //若搜索的位置可以交换
			{
				w[x][y] = w[newx][newy], w[newx][newy] = 0;     //交换空白格位置
				e = change(w);
				if (!vis[e])      //若该状态没有被访问过
				{
					z.data = e;
					vis[z.data] = 1;     //标记访问
					step[z.data] = step[q] + 1;     //层数在原来状态层数上加一
					parent[z.data] = q;      //标记父状态
					getid(z, v);      //获取id值
					open.push(z);     //把搜索的状态放入open表中
				}
				w[newx][newy] = w[x][y], w[x][y] = 0;
			}
		}
		close.pop();
	}
	return -1;
}

int main()
{
	cout << "A*算法：" << endl;
	A u, v;
	int t;
	int** mau, ** mav;
	cout << "输入m*n：" << endl;
	cin >> m >> n;
	mau = new int* [n], mav = new int* [n];
	for (int i = 0; i < n; i++)
		mau[i] = new int[m], mav[i] = new int[m];
	cout << "输入初始状态：" << endl;
	for (int i = 0; i < n; i++)
		for (int j = 0; j < m; j++)
			cin >> mau[i][j];
	cout << "输入最终状态：" << endl;
	for (int i = 0; i < n; i++)
		for (int j = 0; j < m; j++)
			cin >> mav[i][j];
	u.data = change(mau), v.data = change(mav);
	if (Aplus(u, v) != -1)
	{
		cout << "达到目标状态需要： " << Aplus(u, v) << " 步" << endl;
		t = v.data;
		while (t)
		{
			out.push(t);
			t = parent[t];
		}
		while (out.size())
		{
			int** o;
			t = out.top();
			out.pop();
			o = new int* [n];
			for (int i = 0; i < n; i++)
				o[i] = new int[m];
			for (int i = m - 1; i >= 0; i--)
				for (int j = n - 1; j >= 0; j--)
					o[i][j] = t % 10, t /= 10;
			for (int i = 0; i < m; i++)
			{
				for (int j = 0; j < n; j++)
					cout << o[i][j] << " ";
				cout << endl;
			}
			cout << "======" << endl;
		}

	}
	else cout << "无解" << endl;
}

实验结果：

总结心得

广度搜索从四周扩散式地搜索直到搜索到目标节点，比深度搜索效率要高；考虑到深度搜索要是不设置界限值可能要花很长时间才找到目标状态节点，就采取了有界深度搜索，效率比深度搜索要高；启发式搜索相对效率要更高一些，基于广度搜索的算法，在代价函数估计值，找到最接近目标状态的路径去搜索到目标状态。一个状态表示成一维的形式，求出除0之外所有数字的逆序数之和，也就是每个数字前面比它大的数字的个数的和，称为这个状态的逆序。若两个状态的逆序奇偶性相同，则可相互到达，否则不可相互到达。

到此这篇关于利用C++求解八数码问题的文章就介绍到这了,更多相关C++求解八数码问题内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！