解决JavaScript数字精度丢失问题的方法

本文分为三个部分

• JS 数字精度丢失的一些典型问题
• JS 数字精度丢失的原因
• 解决方案（一个对象+一个函数）

一、JS数字精度丢失的一些典型问题

1. 两个简单的浮点数相加

0.1 + 0.2 != 0.3 // true

这真不是 Firebug 的问题，可以用alert试试 （哈哈开玩笑）。

看看Java的运算结果

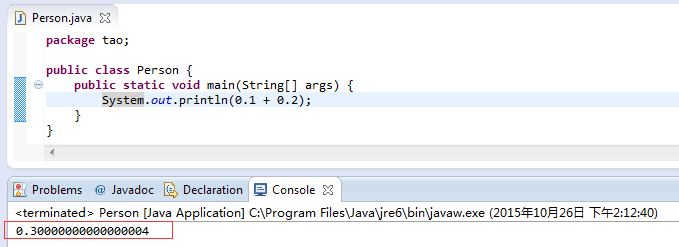
再看看Python

2. 大整数运算

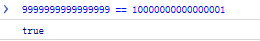
16位和17位数竟然相等，没天理啊。

又如

var x = 9007199254740992
x + 1 == x // ？

看结果

三观又被颠覆了。

3. toFixed 不会四舍五入（Chrome）

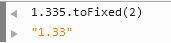
线上曾经发生过 Chrome 中价格和其它浏览器不一致

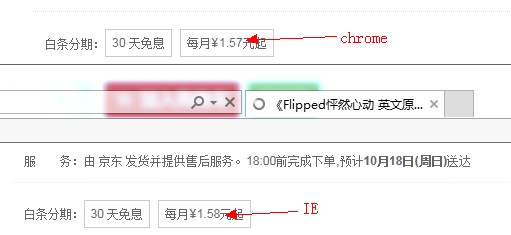
二、JS 数字丢失精度的原因

计算机的二进制实现和位数限制有些数无法有限表示。就像一些无理数不能有限表示，如 圆周率 3.1415926...，1.3333... 等。JS 遵循 IEEE 754 规范，采用双精度存储（double precision），占用 64 bit。如图

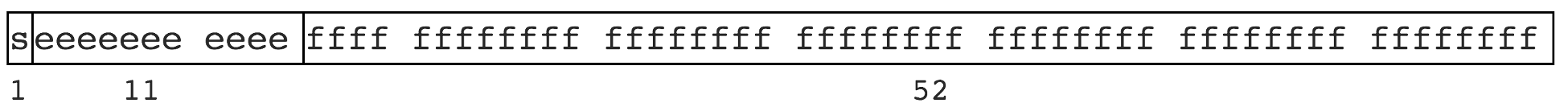
意义

• 1位用来表示符号位
• 11位用来表示指数
• 52位表示尾数

浮点数，比如

0.1 >> 0.0001 1001 1001 1001…（1001无限循环）
0.2 >> 0.0011 0011 0011 0011…（0011无限循环）

此时只能模仿十进制进行四舍五入了，但是二进制只有 0 和 1 两个，于是变为 0 舍 1 入。这即是计算机中部分浮点数运算时出现误差，丢失精度的根本原因。

大整数的精度丢失和浮点数本质上是一样的，尾数位最大是52位，因此 JS 中能精准表示的最大整数是 Math.pow(2, 53)，十进制即 9007199254740992。

大于 9007199254740992 的可能会丢失精度

9007199254740992  >> 10000000000000...000 // 共计 53 个 0
9007199254740992 + 1 >> 10000000000000...001 // 中间 52 个 0
9007199254740992 + 2 >> 10000000000000...010 // 中间 51 个 0

实际上

9007199254740992 + 1 // 丢失
9007199254740992 + 2 // 未丢失
9007199254740992 + 3 // 丢失
9007199254740992 + 4 // 未丢失

结果如图

以上，可以知道看似有穷的数字, 在计算机的二进制表示里却是无穷的，由于存储位数限制因此存在“舍去”，精度丢失就发生了。

三、解决方案

对于整数，前端出现问题的几率可能比较低，毕竟很少有业务需要需要用到超大整数，只要运算结果不超过 Math.pow(2, 53) 就不会丢失精度。

对于小数，前端出现问题的几率还是很多的，尤其在一些电商网站涉及到金额等数据。解决方式：把小数放到位整数（乘倍数），再缩小回原来倍数（除倍数）

// 0.1 + 0.2
(0.1*10 + 0.2*10) / 10 == 0.3 // true

以下是我写了一个对象，对小数的加减乘除运算丢失精度做了屏蔽。当然转换后的整数依然不能超过 9007199254740992。

/**
 * floatObj 包含加减乘除四个方法，能确保浮点数运算不丢失精度
 *
 * 我们知道计算机编程语言里浮点数计算会存在精度丢失问题（或称舍入误差），其根本原因是二进制和实现位数限制有些数无法有限表示
 * 以下是十进制小数对应的二进制表示
 *  0.1 >> 0.0001 1001 1001 1001…（1001无限循环）
 *  0.2 >> 0.0011 0011 0011 0011…（0011无限循环）
 * 计算机里每种数据类型的存储是一个有限宽度，比如 JavaScript 使用 64 位存储数字类型，因此超出的会舍去。舍去的部分就是精度丢失的部分。
 *
 * ** method **
 * add / subtract / multiply /divide
 *
 * ** explame **
 * 0.1 + 0.2 == 0.30000000000000004 （多了 0.00000000000004）
 * 0.2 + 0.4 == 0.6000000000000001 （多了 0.0000000000001）
 * 19.9 * 100 == 1989.9999999999998 （少了 0.0000000000002）
 *
 * floatObj.add(0.1, 0.2) >> 0.3
 * floatObj.multiply(19.9, 100) >> 1990
 *
 */
var floatObj = function() {

 /*
  * 判断obj是否为一个整数
  */
 function isInteger(obj) {
  return Math.floor(obj) === obj
 }

 /*
  * 将一个浮点数转成整数，返回整数和倍数。如 3.14 >> 314，倍数是 100
  * @param floatNum {number} 小数
  * @return {object}
  * {times:100, num: 314}
  */
 function toInteger(floatNum) {
  var ret = {times: 0, num: 0}
  if (isInteger(floatNum)) {
   ret.num = floatNum
   return ret
  }
  var strfi = floatNum + ''
  var dotPos = strfi.indexOf('.')
  var len = strfi.substr(dotPos+1).length
  var times = Math.pow(10, len)
  var intNum = parseInt(floatNum * times + 0.5, 10)
  ret.times = times
  ret.num = intNum
  return ret
 }

 /*
  * 核心方法，实现加减乘除运算，确保不丢失精度
  * 思路：把小数放大为整数（乘），进行算术运算，再缩小为小数（除）
  *
  * @param a {number} 运算数1
  * @param b {number} 运算数2
  * @param digits {number} 精度，保留的小数点数，比如 2, 即保留为两位小数
  * @param op {string} 运算类型，有加减乘除（add/subtract/multiply/divide）
  *
  */
 function operation(a, b, digits, op) {
  var o1 = toInteger(a)
  var o2 = toInteger(b)
  var max = o1.times > o2.times ? o1.times : o2.times
  var result = null
  switch (op) {
   case 'add':
    result = o1.num + o2.num
    break
   case 'subtract':
    result = o1.num - o2.num
    break
   case 'multiply':
    result = o1.num * o2.num
    break
   case 'divide':
    result = o1.num / o2.num
    break
  }
  return result / max
 }

 // 加减乘除的四个接口
 function add(a, b, digits) {
  return operation(a, b, digits, 'add')
 }
 function subtract(a, b, digits) {
  return operation(a, b, digits, 'subtract')
 }
 function multiply(a, b, digits) {
  return operation(a, b, digits, 'multiply')
 }
 function divide(a, b, digits) {
  return operation(a, b, digits, 'divide')
 }

 // exports
 return {
  add: add,
  subtract: subtract,
  multiply: multiply,
  divide: divide
 }

}();

toFixed的修复如下

// toFixed 修复
function toFixed(num, s) {
 var times = Math.pow(10, s)
 var des = num * times + 0.5
 des = parseInt(des, 10) / times
 return des + ''
}

以上就是关于JavaScript数字精度丢失问题全部内容，对典型问题进行分析，分析数字精度丢失原因，还分享了解决方案，希望对大家的学习有所帮助。