C++ 算法精讲之贪心算法

目录

• 选择排序
• 平衡字符串
• 买股票的最佳时机
• 跳跃游戏
• 钱币找零
• 多机调度问题
• 活动选择
• 无重叠区间

选择排序

我们熟知的选择排序，其采用的就是贪心策略。 它所采用的贪心策略即为每次从未排序的数据中选取最小值，并把最小值放在未排序数据的起始位置，直到未排序的数据为0，则结束排序。

void swap(int* arr, int i, int j)
{
	int tmp = arr[i];
	arr[i] = arr[j];
	arr[j] = tmp;
}

void selectSort(int* arr, int n)
{
	//降序
	for (int i = 0; i < n; i++)
	{
		int maxIndex = i;
		for (int j = i+1; j < n; j++)
		{
			if (arr[j] >= arr[maxIndex])
				maxIndex = j;
		}
		swap(arr, i, maxIndex);
	}
}

平衡字符串

问题描述：

在一个 平衡字符串 中，‘L' 和 ‘R' 字符的数量是相同的。

给你一个平衡字符串 s，请你将它分割成尽可能多的平衡字符串。

注意：分割得到的每个字符串都必须是平衡字符串，且分割得到的平衡字符串是原平衡字符串的连续子串。

返回可以通过分割得到的平衡字符串的 最大数量 。

贪心策略：从左往右扫描，只要达到平衡，就立即分割，不要有嵌套的平衡。

故可以定义一个变量balance，在遇到不同的字符时，向不同的方向变化，当balance为0时达到平衡，分割数更新。

比如：从左往右扫描字符串s，遇到L，balance-1，遇到R，balance+1.当balance为0时，更新cnt++ 如果最终cnt==0，说明s只需要保持原样，返回1

代码实现：

class Solution {
public:
    int balancedStringSplit(string s) {
        if(s.size() == 1)
            return 0;
        int cnt = 0;
        int balance = 0;
        for(int i = 0; i < s.size(); i++)
        {
            if(s[i] == 'R')
                --balance;
            else
                ++balance;
            if(balance == 0)
                cnt++;
        }
        if(cnt == 0)
            return 1;

        return cnt;
    }
};

买股票的最佳时机

问题描述：

给定一个数组 prices ，其中 prices[i] 是一支给定股票第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

贪心策略：

连续上涨交易日：第一天买最后一天卖收益最大，等价于每天都买卖。

连续下降交易日：不买卖收益最大，即不会亏钱。

故可以遍历整个股票交易日价格列表，在所有上涨交易日都买卖（赚到所有利润），所有下降交易日都不买卖（永不亏钱）

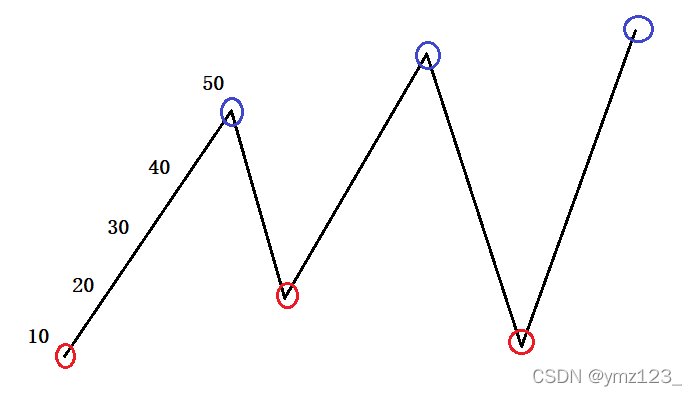
例如从10到50是连续上涨的5天，可以第一天买入，最后一天卖出，利润为40，等价于第一天买入第二天卖出，第二天再买入。。。以此类推

代码实现：

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int profit = 0;
        for(int i = 0; i < prices.size() - 1; i++)
        {
            if(prices[i] <= prices[i+1])
                profit += prices[i+1] - prices[i];
        }

        return profit;
    }
};

跳跃游戏

问题描述：

给定一个非负整数数组 nums ，你最初位于数组的 第一个下标 。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标。

贪心策略：

根据题目描述，对于数组中的任意一个位置y，只要存在一个位置x，它本身可以到达，并且它跳跃的最大长度为x+nums[x]，这个值大于等于y，即x+nums[x] >= y，那么位置y也可以到达。即对于每一个可以到达的位置x，它使得x+1，x+2，…，x+nums[x] >= y，那么位置y也可以到达。 一次遍历数组中的每一个位置，并实时更新最远可以到达的位置。对于当前遍历到的位置x，如果它在最远可以到达的位置范围内，那么我们就可以从起点通过若干次跳跃达到该位置，因此我们可以用x+nums[x]更新最远可以到达的位置。

在遍历的过程中，如果最远可以到达的位置大于等于数组中的最后一个位置，那就说明最后一个位置可到达，直接返回true。遍历结束后，最后一个位置仍不可达，返回false。

例如：[2, 3, 1, 1, 4]

一开始在位置0，可跳跃的最大长度为2，因此最远可以到达的位置倍更新为2；继续遍历到位置1，由于1<=2，因此位置1可达。用1加上它最大可跳跃的长度3，将最远可以到达的位置更新为4，4大于最后一个位置4，返回true

代码实现：

class Solution {
public:
    bool canJump(vector<int>& nums) {
        int maxLen = nums[0];
        for(int i = 0; i < nums.size(); i++)
        {
            if(i <= maxLen)
            {
                maxLen = max(i + nums[i],maxLen);
                if(maxLen >= nums.size() - 1)
                    return true;
            }
        }

        return false;
    }
};

钱币找零

问题描述：

假设1元、2元、5元、10元、20元、50元、100元的纸币分别有c0, c1, c2, c3, c4, c5, c6张。现在要用这些钱来支付K元，至少要用多少张纸币？

贪心策略： 显然，每一步尽可能用面值大的纸币即可。在日常生活中我们也是这么做的。

代码实现：

//按面值降序
struct cmp {
	bool operator()(vector<int>& a1, vector<int>& a2) {
		return a1[0] > a2[0];
	}
};

int solve(vector<vector<int>>& moneyCount, int money)
{
	int num = 0;
	sort(moneyCount.begin(), moneyCount.end(), cmp());
	//首先选择最大面值的纸币
	for (int i = 0; i < moneyCount.size() - 1; i++)
	{
		//选择需要的当前面值和该面值有的数量中的较小值
		int c = min(money / moneyCount[i][0], moneyCount[i][1]);
		money -= c * moneyCount[i][0];
		num += c;
	}
	if (money > 0)
		num = -1;
	return num;
}

多机调度问题

问题描述：

某工厂有n个独立的作业，由m台相同的机器进行加工处理。作业i所需的加工时间为ti，任何作业在被处理时不能中断，也不能进行拆分处理。现厂长请你给他写一个程序：算出n个作业由m台机器加工处理的最短时间。

输入：第一行T（1<T<100)表示有T组测试数据。每组测试数据的第一行分别是整数n，m（1<=n<=10000，1<=m<=100），接下来的一行是n个整数ti（1<=t<=100)。

输出：所需的最短时间

贪心策略：

这个问题还没有最优解，但是用贪心选择策略可设计出较好的近似算法（求次优解） 当n<=m时，只要将作业分给每一个机器即可；当n>m时，首先将n个作业时间从大到小排序，然后依此顺序将作业分配给下一个作业马上结束的处理机。也就是说从剩下的作业中选择需要处理时间最长的，然后依次选择处理时间次长的，直到所有作业全部处理完毕，或者机器不能再处理其他作业为止。如果我们每次是将需要处理时间最短的作业分配给空闲的机器，那么可能就会储秀安其它所有作业都处理完了只剩下所需时间最长的作业在处理的情况，这样势必效率较低。

代码实现：

struct cmp{
	bool operator()(const int& x, const int& y){
		return x > y;
	}
};

int findMax(vector<int>& machines)
{
	int ret = 0;
	for (int i = 0; i < machines.size(); i++)
	{
		if (machines[i] > machines[ret])
			ret = i;
	}

	return machines[ret];
}

int greedStrategy(vector<int>& works, vector<int>& machines)
{
	//降序
	sort(works.begin(), works.end(), cmp());
	int n = works.size();
	int m = machines.size();
	for (int i = 0; i < n; i++)
	{
		int finish = 0;
		int machineTime = machines[finish];
		for (int j = 1; j < m; j++)
		{
			if (machines[j] < machines[finish])
			{
				finish = j;
			}
		}
		machines[finish] += works[i];
	}

	return findMax(machines);
}

活动选择

问题描述：

有n个需要在同一天使用同一个教室的活动a1, a2, …, an，教室同一时刻只能由一个活动使用。每个活动a[i]都有一个开始时间s[i]和结束时间f[i]。一旦被选择后，活动a[i]就占据半开时间区间[s[i],f[i])。如果[s[i],f[i])和[s[j],f[j])互不重叠，a[i]和a[j]两个活动就可以被安排在这一天。求使得尽量多的活动能不冲突的举行的最大数量。

贪心策略：

1.每次都选择开始时间最早的活动，不能得到最优解。

2.每次都选择持续时间最短的活动，不能得到最优解。

3.每次选取结束时间最早的活动（结束时间最早意味着开始时间也早），可以得到最优解。按这种方法选择，可以为未安排的活动留下尽可能多的时间。如下图的活动集合S，其中各项活动按照结束时间单调递增排序。

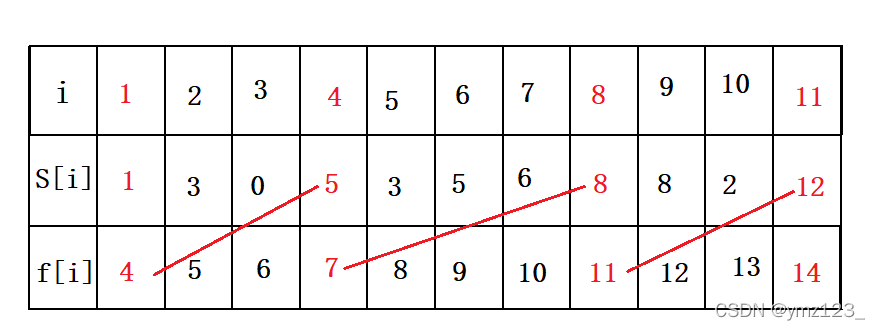
代码实现：

struct cmp{
	bool operator()(vector<int>& s1, vector<int>& s2){
		return s1[1] < s2[1];
	}
};

int getMaxNum(vector<vector<int>>& events)
{
	sort(events.begin(), events.end(), cmp());
	int num = 1;
	int i = 0;
	for (int j = 1; j < events.size();j++)
	{
		if (events[j][0] >= events[i][1])
		{
			++num;
			i = j;
		}
	}

	return num;
}

无重叠区间

问题描述：

给定一个区间的集合，找到需要移除区间的最小数量，使剩余区间互不重叠。

注意:

可以认为区间的终点总是大于它的起点。

区间 [1,2] 和 [2,3] 的边界相互“接触”，但没有相互重叠。

贪心策略：

法一：与上题活动选择类似，用总区间数减去最大可同时进行的区间数即为结果。

法二： 当按照起点先后顺序考虑区间时，利用一个prev指针追踪刚刚添加到最终列表中的区间。遍历时，可能遇到三种情况：

情况1：当前考虑的两个区间不重叠。这种情况下不移除任何区间，将prev赋值为后面的区间，移除区间数量不变。

情况2：两个区间重叠，后一个区间的终点在前一个区间的终点之前。由于后一个区间的长度更小，可以留下更多空间，容纳更多区间，将prev更新为当前区间，移除区间的数量+1

情况3：两个区间重叠，后一个区间的终点在前一个区间的终点之后。直接移除后一个区间，留下更多空间。因此，prev不变，移除区间的数量+1

代码实现： 法一：

struct cmp{
	bool operator()(vector<int>& s1, vector<int>& s2){
		return s1[1] < s2[1];
	}
};

class Solution {
public:
    int eraseOverlapIntervals(vector<vector<int>>& intervals) {
        sort(intervals.begin(), intervals.end(), cmp());
        int num = 1;
        int i = 0;
        for(int j = 1; j < intervals.size(); j++)
        {
            if(intervals[j][0] >= intervals[i][1])
            {
                i = j;
                num++;
            }
        }

        return intervals.size() - num;
    }
};

法二：

struct cmp{
	bool operator()(vector<int>& s1, vector<int>& s2){
		return s1[1] < s2[1];
	}
};

class Solution {
public:
    int eraseOverlapIntervals(vector<vector<int>>& intervals) {
        if(intervals.empty())
            return 0;
        sort(intervals.begin(), intervals.end(), cmp());
        int prev = 0;
        int num = 0;
        for(int i = 1; i < intervals.size(); i++)
        {
            //情况1 不冲突
            if(intervals[i][0] >= intervals[prev][1])
            {
                prev = i;
            }
            else
            {
                if(intervals[i][1] < intervals[prev][1])
                {
                    //情况2
                    prev = i;
                }
                num++;
            }
        }

        return num;
    }
};

到此这篇关于C++ 算法精讲之贪心算法的文章就介绍到这了,更多相关C++ 贪心算法内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！