OpenCV实现霍夫变换直线检测

霍夫变换（Hough Transform）是图像处理中检测是否存在直线的重要算法，该算法是由Paul Hough在1962年首次提出，最开始只能检测图像中的直线，但是霍夫变换经过不断的扩展和完善已经可以检测多种规则形状，例如圆形、椭圆等。霍夫变换通过将图像中的像素在一个空间坐标系中变换到另一个坐标空间坐标系中，使得在原空间中具有形同特性的曲线或者直线映射到另一个空间中形成峰值，从而把检测任意形状的问题转化为统计峰值的问题。

霍夫变换通过构建检测形状的数学解析式将图像中像素点映射到参数空间中，例如我们想检测两个像素点所在的直线，需要构建直线的数学解析式。在图像空间x-y直角坐标系中，对于直线可以用式(7.1)所示的解析式来表示。

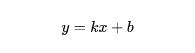
其中k是直线的斜率，b是直线的截距。假设图像中存在一像素点A(x0,y0)，所有经过这个像素点直线可以用式表示。

在图像空间x-y直角坐标系中，由于变量是x和y，因此式表示的是经过点像素点A(x0,y0)的直线，但是经过一点的直线有无数条，因此式中的 和 具有无数个可以选择的值，如果将x0和y0看作是变量， k和 b表示定值，那么式可以表示在k-b空间的一条直线，映射过程示意图如图所示。用式的形式表示映射的结果如式所示，即霍夫变换将x-y直角坐标系中经过一点的所有直线映射成了k-b空间中的一条直线，直线上的每个点都对应着x-y直角坐标系中的一条直线。

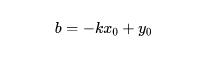
当图像中存在另一个像素点B(x1,y1)时，在图像空间x-y直角坐标系中所有经过像素点B(x1,y1)的直线也会在参数空间中映射出一条直线。由于参数空间中每一个点都表示图像空间x-y直角坐标系中直线的斜率和截距，因此如果有一条直线经过像素点A(x0,y0)和像素点B(x1,y1)时，这条直线所映射在参数空间中的坐标点应该既在像素点A(x0,y0)映射的直线上又在像素点B(x1,y1)映射的直线上。在平面内一个点同时在两条直线上，那么这个点一定是两条直线的交点，因此这条同时经过A(x0,y0)和B(x1,y1)的直线所对应的斜率和截距就是参数空间中两条直线的交点。

根据前面的分析可以得到霍夫变换中存在两个重要的结论：（1）图像空间中的每条直线在参数空间中都对应着单独一个点来表示；（2）图像空间中的直线上任何像素点在参数空间对应的直线相交于同一个点。图给出了第二条结论的示意图。因此通过霍夫变换寻找图像中的直线就是寻找参数空间中大量直线相交的一点。

利用式形式进行霍夫变换可以寻找到图像中绝大多数直线，但是当图像中存在垂直直线时，即所有的像素点的x坐标相同时，直线上的像素点利用上述霍夫变换方法得到的参数空间中多条直线互相平行，无法相交于一点。例如在图像上存在3个像素点(2,1)、(2,2)和(2,3) ，利用式可以求得参数空间中3条直线解析式如式中所示，这些直线具有相同的斜率，因此无法交于一点，具体形式如图所示。

为了解决垂直直线在参数空间没有交点的问题，一般采用极坐标方式表示图像空间x-y直角坐标系中的直线，具体形式如式(7.5)所示。

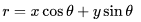
其中 r为坐标原点到直线的距离， Θ为坐标原点到直线的垂线与x轴的夹角，这两个参数的含义如图所示。

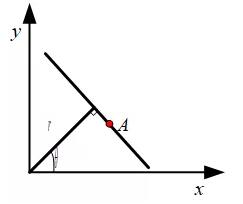
根据霍夫变换原理，利用极坐标形式表示直线时，在图像空间中经过某一点的所有直线映射到参数空间中是一个正弦曲线。图像空间中直线上的两个点在参数空间中映射的两条正弦曲线相交于一点，图中给出了用极坐标形式表示直线的霍夫变换的示意图。

通过上述的变换过程，将图像中的直线检测转换成了在参数空间中寻找某个点 通过的正线曲线最多的问题。由于在参数空间内的曲线是连续的，而在实际情况中图像的像素是离散的，因此我们需要将参数空间的r轴和Θ轴进行离散化，用离散后的方格表示每一条正弦曲线。首先寻找符合条件的网格，之后寻找该网格对应的图像空间中所有的点，这些点共同组成了原图像中的直线。

总结上面所有的原理和步骤，霍夫变换算法检测图像中的直线主要分为4个步骤：

霍夫检测具有抗干扰能力强，对图像中直线的残缺部分、噪声以及其它共存的非直线结构不敏感，能容忍特征边界描述中的间隙，并且相对不受图像噪声影响等优点，但是霍夫变换的时间复杂度和空间复杂度都很高，并且检测精度受参数离散间隔制约。离散间隔较大时会降低检测精度，离散间隔较小时虽然能提高精度，但是会增加计算负担，导致计算时间边长。

标准霍夫变换

void HoughLines( InputArray image, OutputArray lines,
                              double rho, double theta, int threshold,
                              double srn = 0, double stn = 0,
                              double min_theta = 0, double max_theta = CV_PI );

• image：待检测直线的原图像，必须是CV_8U的单通道二值图像。
• lines：霍夫变换检测到的直线输出量，每一条直线都由两个参数表示，分别表示直线距离坐标原点的距离 和坐标原点到直线的垂线与x轴的夹角 。
• rho：以像素为单位的距离分辨率，即距离 离散化时的单位长度。
• theta：以弧度为单位的角度分辨率，即夹角 离散化时的单位角度。
• threshold：累加器的阈值，即参数空间中离散化后每个方格被通过的累计次数大于该阈值时将被识别为直线，否则不被识别为直线。
• srn：对于多尺度霍夫变换算法中，该参数表示距离分辨率的除数，粗略的累加器距离分辨率是第三个参数rho，精确的累加器分辨率是rho/srn。这个参数必须是非负数，默认参数为0。
• stn：对于多尺度霍夫变换算法中，该参数表示角度分辨率的除数，粗略的累加器距离分辨率是第四个参数rho，精确的累加器分辨率是rho/stn。这个参数必须是非负数，默认参数为0。当这个参数与第六个参数srn同时为0时，此函数表示的是标准霍夫变换。
• min_theta：检测直线的最小角度，默认参数为0。
• max_theta：检测直线的最大角度，默认参数为CV_PI，是OpenCV

4中的默认数值具体为3.1415926535897932384626433832795。

该函数用于寻找图像中的直线，并以极坐标的形式将图像中直线的极坐标参数输出。该函数的第一个参数为输入图像，必须是CV_8U的单通道二值图像，如果需要检测彩色图像或者灰度图像中是否存在直线，可以通过Canny()函数计算图像的边缘，并将边缘检测结果二值化后的图像作为输入图像赋值给该参数。函数的第二个参数是霍夫变换检测到的图像中直线极坐标描述的系数，是一个N×2的vector矩阵，每一行中的第一个元素是直线距离坐标原点的距离，第二个元素是该直线过坐标原点的垂线与x轴的夹角，这里需要注意的是图像中的坐标原点在图像的左上角。函数第三个和第四个参数是霍夫变换中对参数空间坐标轴进行离散化后单位长度，这两个参数的大小直接影响到检测图像中直线的精度，数值越小精度越高。第三个参数表示参数空间 轴的单位长度，单位为像素，该参数常设置为1；第四个参数表示参数空间 轴的单位长度，单位为弧度，该函数常设置为CV_PI/180。函数第五个参数是累加器的阈值，表示参数空间中某个方格是否被认定为直线的判定标准，这个数值越大，对应在原图像中构成直线的像素点越多，反之则越少。第六个和第七个参数起到选择标准霍夫变换和多尺度霍夫变换的作用，当两个参数全为0时，该函数使用标准霍夫变换算法，否则该函数使用多尺度霍夫变换算法，当函数使用多尺度霍夫变换算法时，这两个函数分别表示第三个参数单位距离长度的除数和第四个参数角度单位角度的除数。函数最后两个参数是检测直线的最小角度和最大角度，两个参数必须大于等于0小于等于CV_PI（3.1415926535897932384626433832795），并且最小角度的数值要小于最大角度的数值。

该函数只能输出直线的极坐标表示形式的参数。

该函数只能判断图像中是否有直线，而不能判断直线的起始位置

渐进概率式霍夫变换

渐进概率式霍夫变换函数HoughLinesP()可以得到图像中满足条件的直线或者线段两个端点的坐标，进而确定直线或者线段的位置

void HoughLinesP( InputArray image, OutputArray lines,
                               double rho, double theta, int threshold,
                               double minLineLength = 0, double maxLineGap = 0 );

• image：待检测直线的原图像，必须是CV_8C的单通道二值图像。
• lines：霍夫变换检测到的直线输出量，每一条直线都由4个参数进行描述，分别是直线两个端点的坐标
• rho：以像素为单位的距离分辨率，即距离 离散化时的单位长度。
• theta：以弧度为单位的角度分辨率，即夹角 离散化时的单位角度。
• threshold：累加器的阈值，即参数空间中离散化后每个方格被通过的累计次数大于阈值时则被识别为直线，否则不被识别为直线。
• minLineLength：直线的最小长度，当检测直线的长度小于该数值时将会被剔除。
• maxLineGap：允许将同一行两个点连接起来的最大距离。

该函数用于寻找图像中满足条件的直线或者线段两个端点的坐标。该函数的第一个参数为输入图像，必须是CV_8U的单通道二值图像，如果需要检测彩色图像或者灰度图像中是否存在直线，可以通过Canny()函数计算图像的边缘，并将边缘检测结果二值化后的图像作为输入图像赋值给该参数。函数的第二个参数是图像中直线或者线段两个端点的坐标，是一个N×4的vector矩阵。Vec4i中前两个元素分别是直线或者线段一个端点的x坐标和y坐标，后两个元素分别是直线或者线段另一个端点的x坐标和y坐标。函数第三个和第四个参数含义与HoughLines()函数的参数含义相同，都是霍夫变换中对参数空间坐标轴进行离散化后的单位长度，这两个参数的大小直接影响到检测图像中直线的精度，数值越小精度越高。第三个参数表示参数空间 轴的单位长度，单位为像素，该参数常设置为1；第四个参数表示参数空间 轴的单位角度，单位为弧度，该函数常设置为CV_PI/180。函数第五个参数是累加器的阈值，表示参数空间中某个方格是否被认定为直线的判定标准，这个数值越大，对应在原图像中的直线越长，反之则越短。第六个参数是检测直线或者线段的长度，如果图像中直线的长度小于这个阈值，即使是直线也不会作为最终结果输出。函数最后一个参数是邻近两个点连接的最大距离，这个参数主要能够控制倾斜直线的检测长度，当提取较长的倾斜直线时该参数应该具有较大取值。

该函数的最大特点是能够直接给出图像中直线或者线段两个端点的像素坐标，因此可较精确的定位到图像中直线的位置。

在含有坐标点集合中寻找是否存在直线

void HoughLinesPointSet( InputArray _point, OutputArray _lines, int lines_max, int threshold,
                                      double min_rho, double max_rho, double rho_step,
                                      double min_theta, double max_theta, double theta_step );

• _point：输入点的集合，必须是平面内的2D坐标，数据类型必须是CV_32FC2或CV_32SC2。
• _lines：在输入点集合中可能存在的直线，每一条直线都具有三个参数，分别是权重、直线距离坐标原点的距离 和坐标原点到直线的垂线与x轴的夹角 。
• lines_max：检测直线的最大数目。
• threshold：累加器的阈值，即参数空间中离散化后每个方格被通过的累计次数大于阈值时则被识别为直线，否则不被识别为直线。
• min_rho：检测直线长度的最小距离，以像素为单位。
• max_rho：检测直线长度的最大距离，以像素为单位。
• rho_step：：以像素为单位的距离分辨率，即距离 离散化时的单位长度。
• min_theta：检测直线的最小角度值，以弧度为单位。
• max_theta：检测直线的最大角度值，以弧度为单位。
• theta_step：以弧度为单位的角度分辨率，即夹角 离散化时的单位角度。

该函数用于在含有坐标的2D点的集合中寻找直线，函数检测直线使用的方法是标准霍夫变换法。函数第一个参数是2D点集合中每个点的坐标，由于坐标必须是CV_32F或者CV_32S类型，因此可以将点集定义成vector< Point2f>或者vector< Point2f>类型。函数的第二个参数是检测到的输入点集合中可能存在的直线，是一个1×N的矩阵，数据类型为CV_64FC3，其中第1个数据表示该直线的权重，权重越大表示是直线的可靠性越高，第2个数据和第3个数据分别表示直线距离坐标原点的距离 和坐标原点到直线的垂线与x轴的夹角 ，矩阵中数据的顺序是按照权重由大到小依次存放。函数第三个参数是检测直线的数目，如果数目过大，检测到的直线可能存在权重较小的情况。函数第四个参数是累加器的阈值，表示参数空间中某个方格是否被认定为直线的判定标准，这个数值越大，表示检测的直线需要通过的点的数目越多。函数第五个、第六个参数是检测直线长度的取值范围，单位为像素。函数第七个参数是霍夫变换算法中离散化时距离分辨率的大小，单位为像素。函数第八个、第九个参数是检测直线经过坐标原点的垂线与x轴夹角的范围，单位为弧度。函数第七个参数是霍夫变换算法中离散化时角度分辨率的大小，单位为弧度。

简单示例

//
// Created by smallflyfly on 2021/6/21.
//

#include "opencv2/opencv.hpp"
#include <iostream>

using namespace std;
using namespace cv;

void drawLine(const Mat &im, const vector<Vec2f> &lines) {
    Point p1, p2;
    cout << lines.size() << endl;
    for (int i = 0; i < lines.size(); ++i) {
        float rho = lines[i][0];
        float theta = lines[i][1];
        double a = cos(theta);
        double b = sin(theta);
        double x0 = a * rho, y0 = b * rho;
        double length = max(im.rows, im.cols);

        p1.x = cvRound(x0 + length * (-b));
        p1.y = cvRound(y0 + length * a);

        p2.x = cvRound(x0 - length * (-b));
        p2.y = cvRound(y0 - length * a);

        line(im, p1, p2, Scalar(255), 1);
    }
}

int  main() {
    Mat im = imread("road2.jfif");
    resize(im, im, Size(0, 0), 0.5, 0.5);
    cvtColor(im, im, CV_BGR2GRAY);
    imshow("im", im);

    Mat edge;
    Canny(im, edge, 200, 220, 3, false);
    threshold(edge, edge, 125, 255, THRESH_BINARY);

    imshow("edge", edge);

    // 标准霍夫变换
    vector<Vec2f> lines1, lines2;
    HoughLines(edge, lines1, 1, CV_PI/180, 150);
    HoughLines(edge, lines2, 1, CV_PI/180, 100);

    Mat im1, im2;
    im1 = im.clone();
    im2 = im.clone();

    drawLine(im1, lines1);
    drawLine(im2, lines2);

    imshow("im1", im1);
    imshow("im2", im2);

    // 渐进概率式霍夫变换
    Mat im3, im4;
    im3 = im.clone();
    im4 = im.clone();
    vector<Vec4f> lines3, lines4;
    HoughLinesP(edge, lines3, 1, CV_PI/180, 150, 10, 300);
    HoughLinesP(edge, lines4, 1, CV_PI/180, 100, 10, 300);

    for (Vec4f & i : lines3) {
        line(im3, Point(i[0], i[1]), Point(i[2], i[3]),
             Scalar(255, 255, 255), 1);
    }

    for (Vec4f & i : lines4) {
        line(im4, Point(i[0], i[1]), Point(i[2], i[3]),
             Scalar(255, 255, 255), 1);
    }

    imshow("im3", im3);
    imshow("im4", im4);

    // 通过霍夫变换获取点集合中的直线  采用标准霍夫变换
    const static float points[20][2] = {
            { 0.0f,   369.0f },{ 10.0f,  364.0f },{ 20.0f,  358.0f },{ 30.0f,  352.0f },
            { 40.0f,  346.0f },{ 50.0f,  341.0f },{ 60.0f,  335.0f },{ 70.0f,  329.0f },
            { 80.0f,  323.0f },{ 90.0f,  318.0f },{ 100.0f, 312.0f },{ 110.0f, 306.0f },
            { 120.0f, 300.0f },{ 130.0f, 295.0f },{ 140.0f, 289.0f },{ 150.0f, 284.0f },
            { 160.0f, 277.0f },{ 170.0f, 271.0f },{ 180.0f, 266.0f },{ 190.0f, 260.0f }
    };
    vector<Point2f> pts;
    for (auto point : points) {
        pts.emplace_back(point[0], point[1]);
    }
    vector<Vec3d> lines;
    HoughLinesPointSet(pts, lines, 20, 1, 0, 360, 1, 0,
                       CV_PI / 2, CV_PI / 180);

    for (int i = 0; i < lines.size(); ++i) {
        cout << "votes: " << lines[i][0] << ", "
        << "rho: " << lines[i][1] << ", "
        << "theta :" << lines[i][2] << endl;
    }

    waitKey(0);
    destroyAllWindows();

    return 0;
}

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。