Python实现遗传算法(二进制编码)求函数最优值方式

目标函数

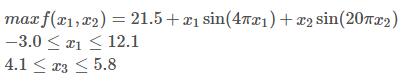
编码方式

本程序采用的是二进制编码精确到小数点后五位，经过计算可知对于 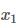其编码长度为18，对于 其编码长度为15，因此每个基于的长度为33。

参数设置

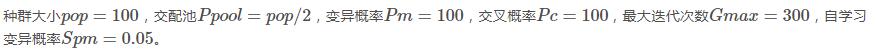
算法步骤

设计的程序主要分为以下步骤：1、参数设置；2、种群初始化；3、用轮盘赌方法选择其中一半较好的个体作为父代；4、交叉和变异；5、更新最优解；6、对最有个体进行自学习操作；7结果输出。其算法流程图为：

算法结果

由程序输出可知其最终优化结果为38.85029，

输出基因编码为[1 1 0 0 1 0 1 1 1 1 1 1 1 0 1 1 1 1 0 1 0 1 1 0 1 0 0 1 0 1 1 1 1]。

代码

import numpy as np
import random
import math
import copy

class Ind():
 def __init__(self):
  self.fitness = 0
  self.x = np.zeros(33)
  self.place = 0
  self.x1 = 0
  self.x2 = 0

def Cal_fit(x, upper, lower): #计算适应度值函数
 Temp1 = 0
 for i in range(18):
  Temp1 += x[i] * math.pow(2, i)
 Temp2 = 0
 for i in range(18, 33, 1):
  Temp2 += math.pow(2, i - 18) * x[i]
 x1 = lower[0] + Temp1 * (upper[0] - lower[0])/(math.pow(2, 18) - 1)
 x2 = lower[1] + Temp2 * (upper[1] - lower[1])/(math.pow(2, 15) - 1)
 if x1 > upper[0]:
  x1 = random.uniform(lower[0], upper[0])
 if x2 > upper[1]:
  x2 = random.uniform(lower[1], upper[1])
 return 21.5 + x1 * math.sin(4 * math.pi * (x1)) + x2 * math.sin(20 * math.pi * x2)
def Init(G, upper, lower, Pop): #初始化函数
 for i in range(Pop):
  for j in range(33):
   G[i].x[j] = random.randint(0, 1)
  G[i].fitness = Cal_fit(G[i].x, upper, lower)
  G[i].place = i
def Find_Best(G, Pop):
 Temp = copy.deepcopy(G[0])
 for i in range(1, Pop, 1):
  if G[i].fitness > Temp.fitness:
   Temp = copy.deepcopy(G[i])
 return Temp

def Selection(G, Gparent, Pop, Ppool): #选择函数
 fit_sum = np.zeros(Pop)
 fit_sum[0] = G[0].fitness
 for i in range(1, Pop, 1):
  fit_sum[i] = G[i].fitness + fit_sum[i - 1]
 fit_sum = fit_sum/fit_sum.max()
 for i in range(Ppool):
  rate = random.random()
  Gparent[i] = copy.deepcopy(G[np.where(fit_sum > rate)[0][0]])

def Cross_and_Mutation(Gparent, Gchild, Pc, Pm, upper, lower, Pop, Ppool): #交叉和变异
 for i in range(Ppool):
  place = random.sample([_ for _ in range(Ppool)], 2)
  parent1 = copy.deepcopy(Gparent[place[0]])
  parent2 = copy.deepcopy(Gparent[place[1]])
  parent3 = copy.deepcopy(parent2)
  if random.random() < Pc:
   num = random.sample([_ for _ in range(1, 32, 1)], 2)
   num.sort()
   if random.random() < 0.5:
    for j in range(num[0], num[1], 1):
     parent2.x[j] = parent1.x[j]
   else:
    for j in range(0, num[0], 1):
     parent2.x[j] = parent1.x[j]
    for j in range(num[1], 33, 1):
     parent2.x[j] = parent1.x[j]
   num = random.sample([_ for _ in range(1, 32, 1)], 2)
   num.sort()
   num.sort()
   if random.random() < 0.5:
    for j in range(num[0], num[1], 1):
     parent1.x[j] = parent3.x[j]
   else:
    for j in range(0, num[0], 1):
     parent1.x[j] = parent3.x[j]
    for j in range(num[1], 33, 1):
     parent1.x[j] = parent3.x[j]
  for j in range(33):
   if random.random() < Pm:
    parent1.x[j] = (parent1.x[j] + 1) % 2
   if random.random() < Pm:
    parent2.x[j] = (parent2.x[j] + 1) % 2

  parent1.fitness = Cal_fit(parent1.x, upper, lower)
  parent2.fitness = Cal_fit(parent2.x, upper, lower)
  Gchild[2 * i] = copy.deepcopy(parent1)
  Gchild[2 * i + 1] = copy.deepcopy(parent2)

def Choose_next(G, Gchild, Gsum, Pop): #选择下一代函数
 for i in range(Pop):
  Gsum[i] = copy.deepcopy(G[i])
  Gsum[2 * i + 1] = copy.deepcopy(Gchild[i])
 Gsum = sorted(Gsum, key = lambda x: x.fitness, reverse = True)
 for i in range(Pop):
  G[i] = copy.deepcopy(Gsum[i])
  G[i].place = i

def Decode(x):   #解码函数
 Temp1 = 0
 for i in range(18):
  Temp1 += x[i] * math.pow(2, i)
 Temp2 = 0
 for i in range(18, 33, 1):
  Temp2 += math.pow(2, i - 18) * x[i]
 x1 = lower[0] + Temp1 * (upper[0] - lower[0]) / (math.pow(2, 18) - 1)
 x2 = lower[1] + Temp2 * (upper[1] - lower[1]) / (math.pow(2, 15) - 1)
 if x1 > upper[0]:
  x1 = random.uniform(lower[0], upper[0])
 if x2 > upper[1]:
  x2 = random.uniform(lower[1], upper[1])
 return x1, x2

def Self_Learn(Best, upper, lower, sPm, sLearn): #自学习操作
 num = 0
 Temp = copy.deepcopy(Best)
 while True:
  num += 1
  for j in range(33):
   if random.random() < sPm:
    Temp.x[j] = (Temp.x[j] + 1)%2
  Temp.fitness = Cal_fit(Temp.x, upper, lower)
  if Temp.fitness > Best.fitness:
   Best = copy.deepcopy(Temp)
   num = 0
  if num > sLearn:
   break
 return Best

if __name__ == '__main__':
 upper = [12.1, 5.8]
 lower = [-3, 4.1]
 Pop = 100
 Ppool = 50
 G_max = 300
 Pc = 0.8
 Pm = 0.1
 sPm = 0.05
 sLearn = 20
 G = np.array([Ind() for _ in range(Pop)])
 Gparent = np.array([Ind() for _ in range(Ppool)])
 Gchild = np.array([Ind() for _ in range(Pop)])
 Gsum = np.array([Ind() for _ in range(Pop * 2)])
 Init(G, upper, lower, Pop)  #初始化
 Best = Find_Best(G, Pop)
 for k in range(G_max):
  Selection(G, Gparent, Pop, Ppool)  #使用轮盘赌方法选择其中50%为父代
  Cross_and_Mutation(Gparent, Gchild, Pc, Pm, upper, lower, Pop, Ppool) #交叉和变异生成子代
  Choose_next(G, Gchild, Gsum, Pop)  #选择出父代和子代中较优秀的个体
  Cbest = Find_Best(G, Pop)
  if Best.fitness < Cbest.fitness:
   Best = copy.deepcopy(Cbest)  #跟新最优解
  else:
   G[Cbest.place] = copy.deepcopy(Best)
  Best = Self_Learn(Best, upper, lower, sPm, sLearn)
  print(Best.fitness)
 x1, x2 = Decode(Best.x)
 print(Best.x)
 print([x1, x2])

以上这篇Python实现遗传算法(二进制编码)求函数最优值方式就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持我们。