python求解汉诺塔游戏

本文实例为大家分享了python求解汉诺塔游戏的具体代码，供大家参考，具体内容如下

一、问题定义

百度百科定义：汉诺塔（又称河内塔）问题是源于印度一个古老传说的益智玩具。据说大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照从小到大顺序摞着64片黄金圆盘。大梵天命令婆罗门借助其中一根柱子，把64片黄金圆盘重新摆放到第三个根柱子上。并且规定，在小黄金圆盘上不能放大的黄金圆盘，在三根柱子之间一次只能移动一个圆盘。

例如，如果黄金圆盘只有3片，则为了满足游戏规则，那么必须按照如下图所示的8个步骤完成：

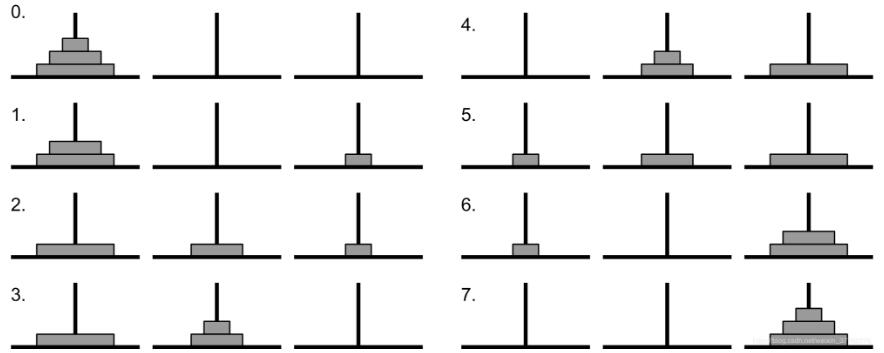
二、代码实现

# 将n个盘子借助y柱从x柱移动到z柱
def hanoi(n, x, y, z):

  count = 0
  if n == 1: # 递归出口
    print(x, ' --> ', z)
    return 1
  else:
    # 将前n - 1个盘子借助z柱从x柱移动到y柱上
    count += hanoi(n - 1, x, z, y) # 递归调用

    # 将最底下的1个盘子从x柱移动到z柱上
    count += hanoi(1, x, y, z)

    # 将n - 1个盘子借助x柱从y柱移动到z柱上
    count += hanoi(n - 1, y, x, z) # 递归调用

    return count

def main():

  hanoi_level = input("请输入汉诺塔层数：")
  print("总共移动次数为%d" % hanoi(int(hanoi_level), 'X', 'Y', 'Z'))

if __name__ == '__main__':
  main()

当黄金圆盘为4层时，代码的输出结果为：

请输入汉诺塔层数：4
X --> Y
X --> Z
Y --> Z
X --> Y
Z --> X
Z --> Y
X --> Y
X --> Z
Y --> Z
Y --> X
Z --> X
Y --> Z
X --> Y
X --> Z
Y --> Z
总共移动次数为15

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。

赞 (0)

相关推荐

  • python益智游戏计算汉诺塔问题示例

    汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具.大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘.大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上.并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘. 复制代码 代码如下: times = 0def test(num,a,b,c):    globaltimes    ifnum==1:       print (a,b)       times+=1 else

  • python实现汉诺塔递归算法经典案例

    python实现汉诺塔递归算法经典案例

    学到递归的时候有个汉诺塔的练习,汉诺塔应该是学习计算机递归算法的经典入门案例了,所以本人觉得可以写篇博客来表达一下自己的见解.这markdown编辑器还不怎么会用,可能写的有点格式有点丑啦,各位看官多多见谅. 网上找了一张汉诺塔的图片,汉诺塔就是利用用中间的柱子把最左边的柱子上的圆盘依次从大到小叠上去,说白了就是c要跟原来的a一样 废话少说,先亮代码 def move(n, a, buffer, c): if(n == 1): print(a,"->",c) return mov

  • Python基于递归算法实现的汉诺塔与Fibonacci数列示例

    Python基于递归算法实现的汉诺塔与Fibonacci数列示例

    本文实例讲述了Python基于递归算法实现的汉诺塔与Fibonacci数列.分享给大家供大家参考,具体如下: 这里我们通过2个例子,学习python中递归的使用. 1. 找出Fibonacci数列中,下标为 n 的数(下标从0计数) Fibonacci数列的形式是这样的:0,1,1,2,3,5,8,13-- ① 使用while循环,python2代码如下: def fib(n): a,b=0,1 count=0 while count<n: a,b=b,a+b count=count+1 pri

  • Python递归实现汉诺塔算法示例

    本文实例讲述了Python递归实现汉诺塔算法.分享给大家供大家参考,具体如下: 最近面试题,面试官让我5分钟实现汉诺塔算法(已然忘记汉诺塔是啥). 痛定思痛,回来查了一下汉诺塔的题目和算法.题干与实现如下: A基座有64个盘子,大在下小在上,每次移动一个盘子,每次都需要大在下小在上,全部移动到B基座,C基座为辅助基座. # -*- coding:utf-8 -*- # 汉诺塔回溯递归实现 # 假设参数中初始杆为a,借助杆为c,阶段终止杆为b # 第一步,a状态借助b移动到c # 第二步,a移动到

  • 使用python实现递归版汉诺塔示例(汉诺塔递归算法)

    利用python实现的汉诺塔.带有图形演示 复制代码 代码如下: from time import sleep def disp_sym(num, sym):        print(sym*num, end='') #recusiondef hanoi(a, b, c, n, tray_num): if n == 1:  move_tray(a, c)  disp(tray_num)  sleep(0.7) else:  hanoi(a, c, b, n-1, tray_num)  move

  • python实现汉诺塔方法汇总

    学习python遇到的第一个问题:汉诺塔问题的实现.首先是不知道什么是汉诺塔问题,然后是不知道怎么实现.于是百度了下,结果如下: 汉诺塔:汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具.大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘.大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上.并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘 方法一: def move(n,a,b,c) # n=2 if n==1 :

  • python实现汉诺塔算法

    题目: 汉诺塔给出最优解,如果对汉诺塔的定义有不了解,请翻看数据结构教材. 除了最基本的之外,还有一题,给定一个数组,arr=[2,3,1,2,3],其含义是这是一个有5个圆盘的汉诺塔,每一个数字代表这个圆盘所在的位置,1代表左边的柱子,2代表中间,3代表右边.给出这个序列代表了汉诺塔移动的第几步,如果该步骤是错误的,则返回-1,所谓错误,是指该步骤不是最简便的得到汉诺塔序列的操作步骤. 分析: 1. 算法当然还是递归解了,即把n个汉诺塔盘子分解成 n - 1 个盘子的移动和一个底层盘子的移动,

  • python实现的汉诺塔算法示例

    python实现的汉诺塔算法示例

    本文实例讲述了python实现的汉诺塔算法.分享给大家供大家参考,具体如下: 规则: 圆盘从下面开始按大小顺序重新摆放在另一根柱子上.并且规定 在小圆盘上不能放大圆盘 在三根柱子之间一次只能移动一个圆盘. 算法思路:[三阶的移动思路] python实现:[注意实参和形参] 用python方法调用,实现输入圆盘数,打印移动的过程 def move(n,a,b,c): if n==1: print(a,'-->',c) else: move(n-1,a,c,b) #将前n-1个盘子从a移动到b上 m

  • python求解汉诺塔游戏

    本文实例为大家分享了python求解汉诺塔游戏的具体代码,供大家参考,具体内容如下 一.问题定义 百度百科定义:汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具.据说大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照从小到大顺序摞着64片黄金圆盘.大梵天命令婆罗门借助其中一根柱子,把64片黄金圆盘重新摆放到第三个根柱子上.并且规定,在小黄金圆盘上不能放大的黄金圆盘,在三根柱子之间一次只能移动一个圆盘. 例如,如果黄金圆盘只有3片,则为了满足游戏规则,那么必须按照如下图所示的

  • python 实现汉诺塔游戏

    一.汉诺塔问题 1. 问题来源 问题源于印度的一个古老传说,大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘.大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上.并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘. 2. 问题阐述 塔内有三个座A.B.C,A座上有64个盘子,盘子从上到下逐渐变大,最下面的盘子最大.目前要把A座的64个盘子从A座移到C座,并且每次只能移动一个盘子,移动过程中三个座保持大盘子在下,小盘子在上,

  • 利用python实现汉诺塔游戏

    利用python实现汉诺塔游戏

    本文实例为大家分享了python实现汉诺塔游戏的具体代码,供大家参考,具体内容如下 一.汉诺塔 汉诺塔问题是一个经典的递归问题,对于这个问题,我们可以把它简单的去看成是如何用n-1去表示n. 在A,B,C三个柱子上,我们先假设A柱上只有两个盘子,那么很简单,只需要把最上面的那个盘子移到B柱上,再把A柱上最下面的盘子移到C柱上,最后把B柱的盘子移到C柱就可以了. 假设我们有n个盘子,那么可以把最下面的盘子看成是第n个盘子,而我们要做的是把上面n-1个盘子移到B柱上,再把第n个盘子移到C柱.我们可以

  • Java编程用栈来求解汉诺塔问题的代码实例（非递归）

    [题目] 汉诺塔问题比较经典,这里修改一下游戏规则:现在限制不能从最左侧的塔直接移动到最右侧,也不能从最右侧直接移动到最左侧,而是必须经过中间.求当塔有N层的时候,打印最优移动过程和最优移动总步数. [解答] 上一篇用的是递归的方法解决这个问题,这里我们用栈来模拟汉诺塔的三个塔,也就是不用递归的方法 原理是这样的:修改后的汉诺塔问题不能让任何塔从左直接移动到右,也不能从右直接移动到左,而是要经过中间,也就是说,实际上能做的动作,只有四个:左->中,中->左,中->右,右->中 用栈

  • c# 实现汉诺塔游戏

    汉诺塔游戏一旦掌握了规律,其实是有点单调和无聊的,不过却是学习递归的一个绝佳例子,想当初学习老谭C的时候,就卡在这儿好长时间. 对初学编程的人来说,递归本身就不易理解,如果使用C语言没有好的调试环境就更难去理解了.在这方面,VS调试输出是真方便,一目了然. 但要想理解递归求解汉诺塔,还是得先玩一玩游戏本身,有点感受.另外,设计一下这个游戏也可以加深对它的理解,同时还可以对数据结构中的栈有一个简单的认识. 因为汉诺塔的游戏规则本身就是一个栈,只能从平台最上面取走碟子,然后放在另一个平台最上面,这明

  • python绘制汉诺塔

    python绘制汉诺塔

    本文实例为大家分享了python绘制汉诺塔的具体代码,供大家参考,具体内容如下 源码: import turtle class Stack: def __init__(self): self.items = [] def isEmpty(self): return len(self.items) == 0 def push(self, item): self.items.append(item) def pop(self): return self.items.pop() def peek(se

  • Java递归来实现汉诺塔游戏,注释详细

    Java递归来实现汉诺塔游戏,注释详细

    我们很容易能想到,可以用递归来实现汉诺塔游戏.因为要将n(n>1)个盘子从"源"柱子移到"目标"柱子,我们要先把n-1个盘子从"源"柱子移到"辅助"柱子上,然后把最底下那一个盘子移到目标柱子上,最后把"辅助柱"上的n-1个盘子移动到目标柱子上.n==1时直接移到目标柱上,也是递归的出口. 有了以上思路的铺垫,就可以开始实现代码了. public class HanoiDemo { public sta

  • Java SE求解汉诺塔问题的示例代码

    Java SE求解汉诺塔问题的示例代码

    目录 1.问题描述 2.画图分析 3.问题讲解 4.代码实现 1.问题描述 汉诺塔问题是一个经典的问题.汉诺塔(Hanoi Tower),又称河内塔,源于印度一个古老传说. 大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘. 大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上. 并且规定,任何时候,在小圆盘上都不能放大圆盘,且在三根柱子之间一次只能移动一个圆盘. 问应该如何操作? 2.画图分析 一个圆盘的情况:移动前 移动后 1个盘子:A直

随机推荐