Java深入分析与解决Top-K问题

目录

• 题目
• 解题方案
• 方法一
• 方法二
• 方法三

题目

求最小的K个数

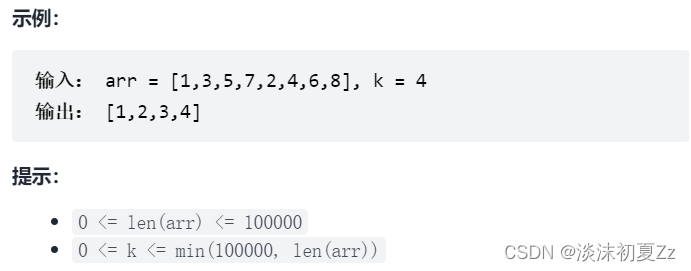
设计一个算法，找出数组中最小的k个数。以任意顺序返回这k个数均可。

解题方案

方法一

排序（冒泡/选择）

思路

1，冒泡排序是每执行一次，就会确定最终位置，执行K次后，就可以得到结果，时间复杂度为O(n * k),当k<<n时，O(n * k)的性能会比O(N*logN)好。

2，选择排序每执行依次，就会通过确定一个最大的或最小的放在一端，通过选择排序，执行K次就可以得到最大的K个数了。时间复杂度时O(N * K)。

代码实现

  //冒泡排序
    public static int[] topKByBubble(int[] arr, int k) {
        int[] ret = new int[k];
        if (k == 0 || arr.length == 0) {
            return ret;
        }
        for (int i = 0; i < k; i++) {
            for (int j = arr.length - 1; j < i; j--) {
                if (arr[j] > arr[j + 1]) {
                    swap(arr, j, j + 1);
                }
            }
            ret[i] = arr[i];
        }
        return ret;
    }
    //选择排序
    public static int[] topKBySelect(int[] arr, int k) {
        int[] ret = new int[k];
        for (int i = 0; i < k; i++) {
            int maxIndex = i;
            int maxNum = arr[maxIndex];
            for (int j = i + 1; j < arr.length; j++) {
                if (arr[j] > maxNum) {
                    maxIndex = j;
                    maxNum = arr[j];
                }
            }
            if (maxIndex != i) {
                swap(arr, maxIndex, i);
            }
            ret[i] = arr[i];
        }
        return ret;
    }
    public static void swap(int[] arr, int a, int b) {
        int temp = arr[a];
        arr[a] = arr[b];
        arr[b] = temp;
    }

方法二

分治-快速排序

思路

1，快速排序的核心是分治思想，先通过分治partition把序列分为两个部分，再将两个部分进行再次递归；

2,利用分治思想，即划分操作partition，根据主元素pivot调整序列，比pivot大的放在左端，比pivot小的放在右端，这样确定主元素pivot的位置pivotIndex，如果pivotIndex刚好是k-1，那么前k-1位置的数就是前k大的元素，即我们要求的top K。

时间复杂度: O(n)

代码实现

public static int[] topKByPartition(int[] arr, int k){
    if(arr.length == 0 || k <= 0){
        return new int[0];
    }
    return quickSort(arr,0,arr.length-1,k);

}
//快速排序
public static int[] quickSort(int[] arr, int low, int high, int k){
    int n = arr.length;
    int pivotIndex = partition(arr, low, high);
    if(pivotIndex == k-1){
        return Arrays.copyOfRange(arr,0,k);
    }else if(pivotIndex > k-1){
        return quickSort(arr,low,pivotIndex-1,k);
    }else {
        return quickSort(arr,pivotIndex+1,high,k);
    }
}
public static int partition(int[] arr, int low, int high){
   if(high - low == 0){
       return low;
   }
   int pivot = arr[high];
   int left = low;
   int right = high-1;
   while (left < right){
       while (left < right && arr[left] > pivot){
           left++;
       }
       while (left < right && arr[right] < pivot){
           right--;
       }
       if(left < right){
           swap(arr,left,right);
       }else {
           break;
       }
   }
   swap(arr,high,left);
   return left;
}
public static void swap(int[] arr,int a, int b){
    int temp = arr[a];
    arr[a] = arr[b];
    arr[b] = temp;
}

方法三

利用堆

思路

1，构建一个最大堆

2，遍历原数组，元素入队，当堆的大小为K时，只需要将堆顶元素于下一个元素比较，如果大于堆顶元素，则将堆顶元素删除，将该元素插入堆中，直到遍历完所有元素

3，将queue存储的K个数出队

时间复杂度：为O(N*logK)

代码实现

public class TopK {
    public int[] smallestK(int[] arr, int k) {
        int[] ret = new int[k];
        if(k==0 || arr.length==0){
            return ret;
        }
        // 1,构建一个最大堆
        // JDK的优先级队列是最小堆， 就要用到我们比较器
        Queue<Integer> queue = new PriorityQueue<>(new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return o2 - o1;
            }
        });
        //2,遍历原数组，进行入队
        for(int value:arr){
            if(queue.size() < k){
                queue.offer(value);
            }else{
                if(value < queue.peek()){
                    queue.poll();
                    queue.offer(value);
                }
            }
        }
        //3,将queue中存储的K个元素出队
        for(int i = 0;i < k;i++){
            ret[i] = queue.poll();
        }
        return ret;
    }
}

到此这篇关于Java深入分析与解决Top-K问题的文章就介绍到这了,更多相关Java Top-K内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！