如何利用Python动态展示排序算法

目录

• 前言
• 选择冒泡
• 插入排序
• 归并排序
• 希尔排序
• 总结

前言

经常看到这种算法可视化的图片，但往往做不到和画图的人心灵相通，所以想自己画一下，本文主要实现归并排序和希尔排序，如果想实现其他算法可参考这篇

C语言实现各种排序算法[选择，冒泡，插入，归并，希尔，快排，堆排序，计数]

选择冒泡

这两种排序方案简单到很难说是什么算法，其中选择排序通过遍历一次数组，选出其中最大（小）的值放在新数组的第一位,再从剩下的数里选出最大（小）的，放到第二位，依次类推；冒泡排序则是通过重复走访要排序的数组，比较相邻元素，如果顺序不符合要求则交换位置，直到不需要交换为止。

选择排序

  冒泡排序

二者的核心代码分别为：

#x为待排序列表，N=len(x)
#选择排序
for i in range(N):
    iMax = i
    for j in range(i, N):
        if(x[j]>x[iMax]):
            iMax = j
    x[iMax],x[i] = x[i],x[iMax]

#冒泡排序
tempN = N-1
for i in range(tempN):
    for j in range(0, tempN-i):
        if(x[j]>x[j+1]):
            x[j],x[j+1] = x[j+1],x[j]

下面给出选择排序的绘图代码，其他的所有排序算法，其实只需改变核心部分。

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation 

start,end,N = 10,100,9
x = np.random.randint(start, end, size=N)
Index = np.arange(N)
xs = []
nowIndex = []

for i in range(N):
    iMax = i
    for j in range(i, N):
        xs.append(x*1)      #存储当前顺序，用于绘图
        nowIndex.append([i,j,iMax]) #存储当前的i,j,max位置，用于绘图
        if(x[j]>x[iMax]):
            iMax = j
            xs.append(x*1)
            nowIndex.append([i,j,iMax])
    x[iMax],x[i] = x[i],x[iMax]

fig, ax = plt.subplots()
colors = np.repeat('g',N)
colors[0] = 'b'
bar = ax.bar(Index,x,color=colors)

def animate(n):
    data = xs[n]
    colors = np.repeat('gray',N)
    colors[nowIndex[n]] = 'b','g','r'
    ax.clear()
    bar = ax.bar(Index, data, color=colors)
    return bar

ani = animation.FuncAnimation(fig, animate,
    range(len(xs)), interval=500, repeat=False, blit=True)
plt.show()
ani.save("sort.gif")

插入排序

插入排序的基本思路是将数组分为前后两个部分，前面有序，后面无序。逐个扫描无序数组，将每次扫描的数插入到有序数组中，从而有序数组越来越长，无序数组越来越短，直到整个数组都是有序的。

核心代码为

for i in range(1,N):
    j = i-1
    temp = x[i]
    while(x[i]<x[j] and j>=0):
        x[j+1] = x[j]
        j -= 1
    x[j+1] = temp

由于在这段代码中，x[i]被取出放在旁边，所以其动态图中大部分时间会缺失一个值，在图中将其置于最右侧，其动态过程如图所示，蓝色表示抽出来准备插进去的那根bar

归并排序

排序算法到这里才算有点意思，归并排序是算法导论中介绍分治概念时提到的，基本思路是将数组拆分成子数组，然后令子数组有序，再令数组之间有序，从而整个数组有序。

算法步骤

设数组有 n个元素， { a 0 , a 1 , … , a n }

1. 如果数组元素大于2，则将数组分成左数组和右数组，如果数组等于2，则将数组转成有序数组
2. 对左数组和右数组执行1操作。
3. 合并左数组和右数组。

可以发现，对长度为 n 的数组，需要 log ₂ n 次的拆分，每个拆分层级都有 O ( n ) 的时间复杂度和 O ( n )的空间复杂度，所以其时间复杂度和空间复杂度分别为 O ( n log ₂ n ) 和 O ( n ) 。

其核心算法为

def Merge(X, Y):
    nL,nR = len(X), len(Y)
    iterL,iterR = 0,0
    xNew = []
    for _ in range(nL+nR):
        if(iterL==nL): return xNew + Y[iterR:]
        if(iterR==nR): return xNew + X[iterL:]
        if(X[iterL]<Y[iterR]):
            xNew.append(X[iterL])
            iterL += 1
        else:
            xNew.append(Y[iterR])
            iterR += 1
    return xNew

def MergeSort(x):
    if len(x)==1:
        return x
    if len(x)==2:
        return x if x[0]<x[1] else [x[1],x[0]]
    nL = len(x)//2
    return Merge(MergeSort(x[:nL]),
                 MergeSort(x[nL:]))

当然这么写效率是非常低的，如果像高效还是得用指针，但我都已经用Python了，所以就不去想效率的问题，问题的关键是这种带有返回值的递归程序根本没法画图啊。。。所以还是改成指针的写法

def Merge(X, nL):
    nR = len(X)-nL
    XL,XR = X[:nL]*1,X[nL:]*1
    iterL,iterR = 0,0
    for i in range(nL+nR):
        if(iterL==nL): break
        if(iterR==nR):
            X[i:] = XL[iterL:]
            return
        if(XL[iterL]<XR[iterR]):
            X[i] = XL[iterL]
            iterL += 1
        else:
            X[i] = XR[iterR]
            iterR += 1

def MergeSort(X):
    if len(X)<2:
        return
    nL = len(X)//2
    MergeSort(X[:nL])
    MergeSort(X[nL:])
    Merge(X,nL)

这个图。。怎么说呢，因为在Merge过程中，有很多bar被掩盖掉了，所以可能只有画图的人能看懂吧。。。

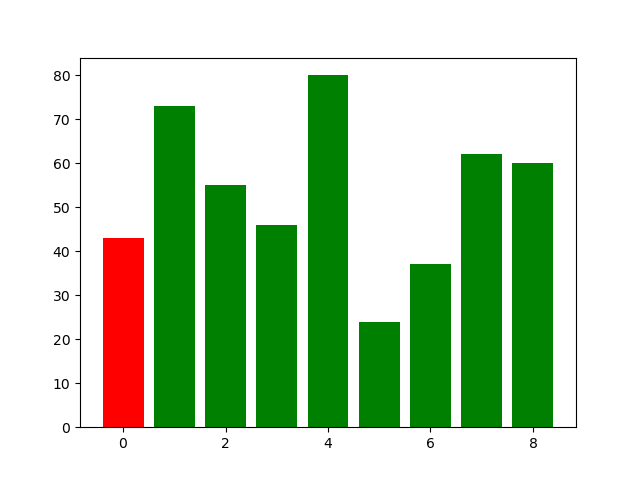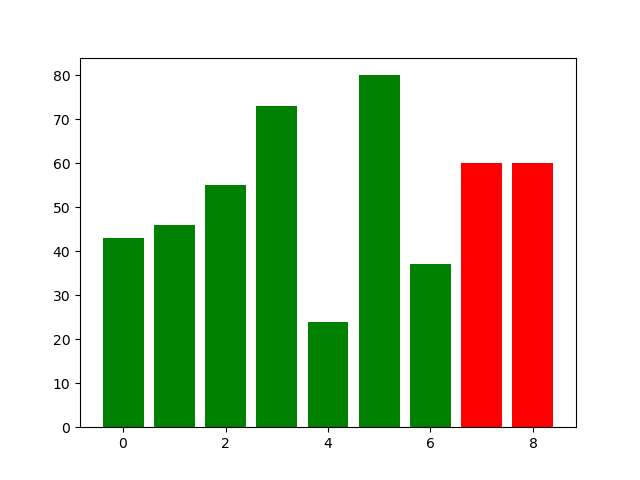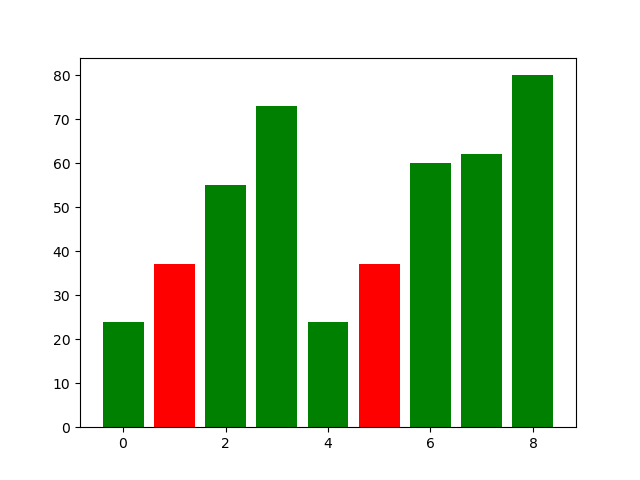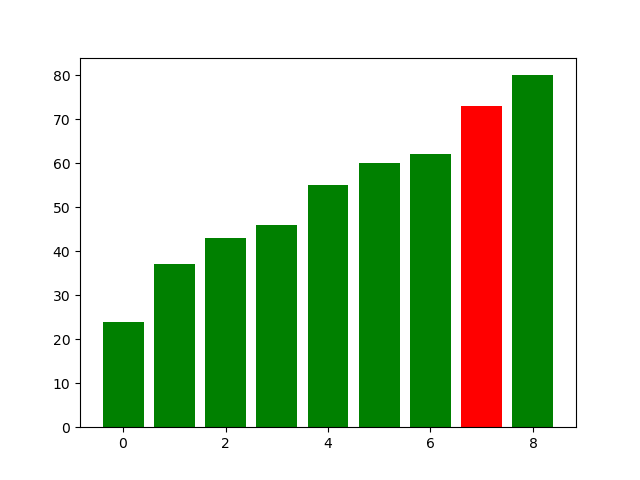
希尔排序

据说是第一个突破 O ( n ² ) 的排序算法，又称为缩小增量排序，本质上也是一种分治方案。

在归并排序中，先将长度为n的数组划分为nL和nR两部分，然后继续划分，直到每个数组的长度不大于2，再对每个不大于2的数组进行排序。这样，每个子数组内部有序而整体无序，然后将有序的数组进行回溯重组，直到重新变成长度为n的数组为止。

希尔排序反其道而行之，在将数组划分为nL和nR后，对nL和nR进行按位排序，使得nL和nR内部无序，但整体有序。然后再将数组进行细分，当数组长度变成1的时候，内部也就谈不上无序了，而所有长度为1的数组整体有序，也就是说有这些子数组所组成的数组是有序的。

算法步骤

设数组有 n 个元素， { a 0 , a 1 , … , a n }

1. 如果数组元素大于2，则将数组分成左数组和右数组，并对左数组和右数组的元素进行一对一地排序。
2. 对每一个数组进行细分，然后将每个子数组进行一对一排序。

def ShellSort(arr):
    n = len(arr)
    nSub = n//2
    while nSub>0:
        for i in range(nSub,n):
            temp = arr[i]
            j = i-nSub
            while j>=0 and temp<arr[j]:
                arr[j+nSub] = arr[j]
                j -= nSub
            arr[j+nSub] = temp
        nSub //= 2

总结

到此这篇关于如何利用Python动态展示排序算法的文章就介绍到这了,更多相关Python动态展示排序算法内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！