一文详解Python灰色预测模型实现示例

目录

• 前言
• 一、模型理论
• 特点
• 二、模型场景
• 1.预测种类
• 2.适用条件
• 三、建模流程
• 1.级比校验
• 3.系数求解
• 4.残差检验与级比偏差检验
• 四、Python实例实现
• 总结

前言

博主参与过大大小小十次数学建模比赛，也获得了不少建模奖项。对于一些小批量样本数据去做预测或者是评估其规律性的话，比较适合的模型一般都是选择灰色预测模型。该模型解释性强而且易于理解，建模手段也比较简单。在一些不确定是否存在相关标量或者是存在位置特征的时候，用灰色预测模型尤为明显，牵扯太多变量时候可以以量曾量减的方式显现其变化规律，是建模比较好用的算法和思路。但是首先我们要明白该模型的使用场景以及优缺点才能更好的解释建模的效果。故为接下来的美赛，我将把一些常用建模的模型和代码补上。

一、模型理论

灰色预测模型是通过少量的、不完全的信息，建立数学模型做出预测的一种预测方法。是基于客观事物的过去和现在的发展规律，借助于科学的方法对未来的发展趋势和状况进行描述和分析，并形成科学的假设和判断。

我们称信息完全未确定的系统为黑色系统，称信息完全确定的系统为白色系统，灰色系统就是这介于这之间，一部分信息是已知的，另一部分信息是未知的，系统内各因素间有不确定的关系。

不知道大家知不知道白盒测试和黑盒测试，我们可以这样通俗的理解，黑色系统就好比一个黑色的盒子你看不到里面装着几个小球，从里面拿出几个小球或者是章鱼都是未知数。而白色系统就像是透明的盒子，你能很清楚的看到里面是什么你想要拿什么出来拿多少个。而这个灰色系统介于他们之间，盒子是灰色的，只能模糊的看到一些小球，看不到几个或者是有除了小球以外的其他东西。

灰色预测通过鉴别系统因素之间发展趋势的相异程度，即进行关联分析，并对原始数据进行生成处理来寻找系统变动的规律，生成有较强规律性的数据序列，然后建立相应的微分方程模型，从而预测事物未来发展趋势的状况。其用等时距观测到的反映预测对象特征的一系列数量值构造灰色预测模型，预测未来某一时刻的特征量，或达到某一特征量的时间。

特点

• 用灰色数学处理不确定量，使之量化。
• 充分利用已知信息寻求系统的运动规律。
• 灰色系统理论能处理贫信息系统。

二、模型场景

1.预测种类

• 灰色时间序列预测；即用观察到的反映预测对象特征的时间序列来构造灰色预测模型，预测未来某一时刻的特征量，或达到某一特征量的时间。
• 畸变预测；即通过灰色模型预测异常值出现的时刻，预测异常值什么时候出现在特定时区内。
• 系统预测；通过对系统行为特征指标建立一组相互关联的灰色预测模型，预测系统中众多变量间的相互协调关系的变化。
• 拓扑预测；将原始数据作曲线，在曲线上按定值寻找该定值发生的所有时点，并以该定值为框架构成时点序列，然后建立模型预测该定值所发生的时点。

2.适用条件

灰色预测模型可针对数量非常少（比如仅4个），数据完整性和可靠性较低的数据序列进行有效预测，其利用微分方程来充分挖掘数据的本质，建模所需信息少，精度较高，运算简便，易于检验，也不用考虑分布规律或变化趋势等。但灰色预测模型一般只适用于短期预测，只适合指数增长的预测，比如人口数量，航班数量，用水量预测，工业产值预测等。

三、建模流程

总体建模流程可以参考：

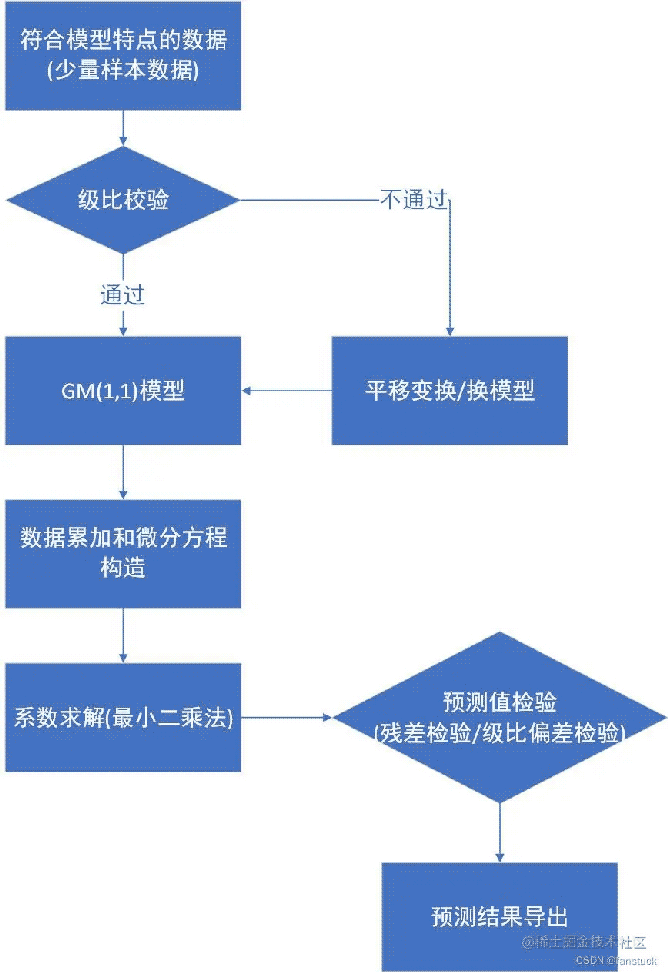
1.级比校验

trong>数据累加和微分方程构造

3.系数求解

数据向量Y：

4.残差检验与级比偏差检验

四、Python实例实现

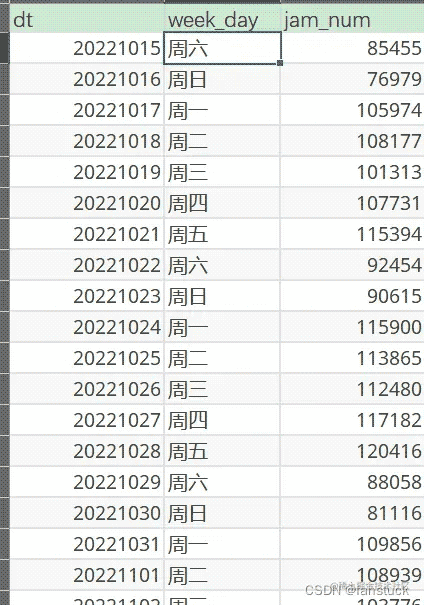
我们通过得到的周数拥堵车辆数据进行测试：

import numpy as np
import pandas as pd
from decimal import *
import matplotlib.pyplot as plt
def Grade_ratio_test(X0):
    lambds = [X0[i - 1] / X0[i] for i in range(1, len(X0))]
    X_min = np.e ** (-2 / (len(X0) + 1))
    X_max = np.e ** (2 / (len(X0) + 1))
    for lambd in lambds:
        if lambd < X_min or lambd > X_max:
            print('该数据未通过级比检验')
            return False
    print('该数据通过级比检验')
    return True
def model_train(X0_train):
    #AGO生成序列X1
    X1 = X0_train.cumsum()
    Z= (np.array([-0.5 * (X1[k - 1] + X1[k]) for k in range(1, len(X1))])).reshape(len(X1) - 1, 1)
    # 数据矩阵A、B
    A = (X0_train[1:]).reshape(len(Z), 1)
    B = np.hstack((Z, np.ones(len(Z)).reshape(len(Z), 1)))
    # 求灰参数
    a, u = np.linalg.inv(np.matmul(B.T, B)).dot(B.T).dot(A)
    u = Decimal(u[0])
    a = Decimal(a[0])
    print("灰参数a：", a, "，灰参数u：", u)
    return u,a
def model_predict(u,a,k,X0):
    predict_function =lambda k: (Decimal(X0[0]) - u / a) * np.exp(-a * k) + u / a
    X1_hat = [float(predict_function(k)) for k in range(k)]
    X0_hat = np.diff(X1_hat)
    X0_hat = np.hstack((X1_hat[0], X0_hat))
    return X0_hat
'''
根据后验差比及小误差概率判断预测结果
:param X0_hat: 预测结果
:return:
'''
def result_evaluate(X0_hat,X0):
    S1 = np.std(X0, ddof=1)  # 原始数据样本标准差
    S2 = np.std(X0 - X0_hat, ddof=1)  # 残差数据样本标准差
    C = S2 / S1  # 后验差比
    Pe = np.mean(X0 - X0_hat)
    temp = np.abs((X0 - X0_hat - Pe)) < 0.6745 * S1
    p = np.count_nonzero(temp) / len(X0)  # 计算小误差概率
    print("原数据样本标准差：", S1)
    print("残差样本标准差：", S2)
    print("后验差比：", C)
    print("小误差概率p：", p)
if __name__ == '__main__':
    plt.rcParams['font.sans-serif'] = ['SimHei']  # 步骤一（替换sans-serif字体）
    plt.rcParams['axes.unicode_minus'] = False  # 步骤二（解决坐标轴负数的负号显示问题）
        # 原始数据X
    data = pd.read_excel('./siwei_day_traffic.xlsx')
    X=data[data['week_day']=='周五'].jam_num[:5].astype(float).values
    print(X)
    # 训练集
    X_train = X[:int(len(X) * 0.7)]
    # 测试集
    X_test = X[int(len(X) * 0.7):]
    Grade_ratio_test(X_train)  # 判断模型可行性
    a,u=model_train(X_train)  # 训练
    Y_pred = model_predict(a,u,len(X),X)  # 预测
    Y_train_pred = Y_pred[:len(X_train)]
    Y_test_pred = Y_pred[len(X_train):]
    score_test = result_evaluate(Y_test_pred, X_test)  # 评估
    # 可视化
    plt.grid()
    plt.plot(np.arange(len(X_train)), X_train, '->')
    plt.plot(np.arange(len(X_train)), Y_train_pred, '-o')
    plt.legend(['负荷实际值', '灰色预测模型预测值'])
    plt.title('训练集')
    plt.show()
    plt.grid()
    plt.plot(np.arange(len(X_test)), X_test, '->')
    plt.plot(np.arange(len(X_test)), Y_test_pred, '-o')
    plt.legend(['负荷实际值', '灰色预测模型预测值'])
    plt.title('测试集')
    plt.show()

总结

模型优点：数据少且无明显规律时可用，利用微分方程挖掘数据本质规律。

模型缺点：灰色预测只适合短期预测、指数增长的预测。

以上就是一文详解Python灰色预测模型实现示例的详细内容，更多关于Python灰色预测模型的资料请关注我们其它相关文章！